VIDEO
Математика - Производная // Skill up
VIDEO
Телекинокурс. Высшая математика. Лекции 25-26. Дифференциал. Фильм 02 (1973) [1:05:18]
Производная — математический термин , обозначающий некую функцию, соответствующую скорости изменения функции .
Нахождение производной от функции называется дифференцированием .
1. Определение производной через понятие дифференциала .
Производная от функции y = f(x) равна отношению дифференциалов функции и аргумента.
y
′
(
x
)
=
d
y
d
x
{\displaystyle y'(x)={\frac {dy}{dx}}}
2. Определение производной от функции через понятие предела .
Производная от функции y = f(x) равна пределу отношения приращения функции Δy к приращению аргумента Δx , когда приращение аргумента стремится к нулю Δx → 0 .
y
′
(
x
)
=
lim
Δ
x
→
0
Δ
y
Δ
x
⇔
y
′
(
x
)
=
lim
Δ
x
→
0
y
(
x
+
Δ
x
)
−
y
(
x
)
Δ
x
{\displaystyle y'(x)=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}\Leftrightarrow y'(x)=\lim _{\Delta x\to 0}{\frac {y(x+\Delta x)-y(x)}{\Delta x}}}
f
′
(
x
)
=
lim
Δ
x
→
0
Δ
f
Δ
x
⇔
f
′
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle f'(x)=\lim _{\Delta x\to 0}{\frac {\Delta f}{\Delta x}}\Leftrightarrow f'(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
Производные элементарных функций
Производные сложных функций
Свойства производных [ править ] Для функций u=f(x) и v=g(x) верны правила:
При f(x) и g(x)=C получаем:
При f(x)=C и g(x) получаем:
Формулы сложных функций [ править ]
[
f
(
g
(
x
)
)
]
x
′
=
f
g
′
(
g
(
x
)
)
⋅
g
x
′
(
x
)
⇔
[
u
(
v
)
]
x
′
=
u
v
′
⋅
v
x
′
{\displaystyle \left[f(g(x))\right]'_{x}=f'_{g}(g(x))\cdot g'_{x}(x)\Leftrightarrow \left[u(v)\right]'_{x}=u'_{v}\cdot v'_{x}}
[
f
(
x
)
g
(
x
)
)
]
x
′
=
f
(
x
)
g
(
x
)
⋅
[
f
x
′
(
x
)
⋅
g
(
x
)
f
(
x
)
+
g
x
′
(
x
)
⋅
ln
f
(
x
)
]
⇔
[
u
v
]
x
′
=
u
v
⋅
(
u
x
′
v
u
+
v
x
′
ln
u
)
{\displaystyle \left[f(x)^{g(x)})\right]'_{x}=f(x)^{g(x)}\cdot \left[f'_{x}(x)\cdot {\frac {g(x)}{f(x)}}+g'_{x}(x)\cdot \ln f(x)\right]\Leftrightarrow \left[u^{v}\right]'_{x}=u^{v}\cdot \left(u'_{x}{\frac {v}{u}}+v'_{x}\ln u\right)}
Другие понятия [ править ]
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970. 


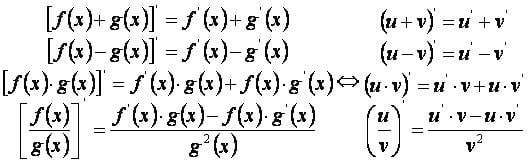
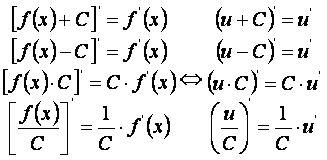
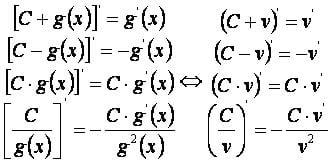
![{\displaystyle \left[f(g(x))\right]'_{x}=f'_{g}(g(x))\cdot g'_{x}(x)\Leftrightarrow \left[u(v)\right]'_{x}=u'_{v}\cdot v'_{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebe540fdd3d29e54642c7883c6cf99edaf773904)
![{\displaystyle \left[f(x)^{g(x)})\right]'_{x}=f(x)^{g(x)}\cdot \left[f'_{x}(x)\cdot {\frac {g(x)}{f(x)}}+g'_{x}(x)\cdot \ln f(x)\right]\Leftrightarrow \left[u^{v}\right]'_{x}=u^{v}\cdot \left(u'_{x}{\frac {v}{u}}+v'_{x}\ln u\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4332a9dda641cfbb48db1dc20ded13f4fcd58792)