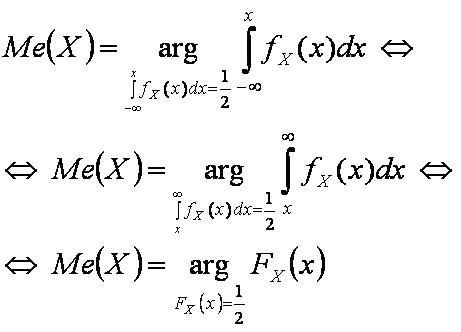Медиана непрерывной случайной величины

Основные формулы

Медиана, для непрерывной случайной величины — числовая характеристика случайной величины, равная значению (случайной величины) для которого вероятность меньших значений равна вероятности больших значений.

Обозначения

X — случайная величина;

f_X(x) — дифференциальная функция распределения — функция плотности вероятности;

F_X(x) — интегральная функция распределения — функция вероятности;

Me(X) — медиана.

Формулы

$Me(X)=\arg \limits _{\int \limits _{-\infty }^{x}f_{X}(x)dx={\frac {1}{2}}}\ \int \limits _{-\infty }^{x}f_{X}(x)dx\Leftrightarrow$

$\Leftrightarrow Me(X)=\arg \limits _{\int \limits _{x}^{\infty }f_{X}(x)dx={\frac {1}{2}}}\ \int \limits _{x}^{\infty }f_{X}(x)dx\Leftrightarrow$

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \Leftrightarrow Me(X)=\arg \limits _{F_{X}(x)={\frac {1}{2}}}F_{X}(x)}

См. также

• Медиана дискретной случайной величины

Другие формулы

1. средняя;
2. дисперсия;
3. среднеквадратическое отклонение;
4. среднее линейное отклонение;
5. мода;
6. медиана;
7. квартиль;
8. дециль;
9. начальный момент k-ого порядка;
10. центральный момент k-ого порядка;
11. коэффициент асимметрии;
12. коэффициент эксцесса.