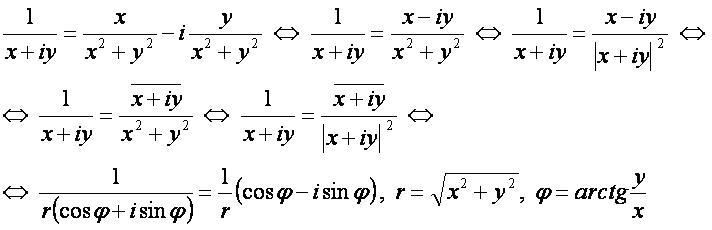Обращение комплексного числа

Формула

Обращение комплексного числа — это результат операции взятие обратного (по умножению) комплексного числа. Его можно представлять как результат операции деления 1 на исходное число и он равен нормированному сопряжённому исходному числу, делённому на модуль исходного числа.

Обозначения

Введём обозначения:

x — действительная часть (абсцисса) числа;

y — мнимая часть (ордината) числа;

r — модуль комплексного числа;

φ — аргумент комплексного числа;

x + iy — комплексное число.

Формула

${\frac {1}{x+iy}}={\frac {x}{x^{2}+y^{2}}}-i{\frac {y}{x^{2}+y^{2}}}\Leftrightarrow {\frac {1}{x+iy}}={\frac {x-iy}{x^{2}+y^{2}}}\Leftrightarrow {\frac {1}{x+iy}}={\frac {x-iy}{\left|x+iy\right|^{2}}}\Leftrightarrow$

$\Leftrightarrow {\frac {1}{x+iy}}={\frac {\overline {x+iy}}{x^{2}+y^{2}}}\Leftrightarrow {\frac {1}{x+iy}}={\frac {\overline {x+iy}}{\left|x+iy\right|^{2}}}\Leftrightarrow$

$\Leftrightarrow {\frac {1}{r(\cos \varphi +i\sin \varphi )}}={\frac {1}{r}}(\cos \varphi -i\sin \varphi ),\ r={\sqrt {x^{2}+y^{2}}},\ \varphi =arctg{\frac {y}{x}}$

Другие операции

• сложение чисел;
• вычитание чисел;
• умножение чисел;
• деление чисел;
• обращение числа;
• возведение в степень;
• извлечение квадратного корня;
• извлечение кубического корня;
• извлечение корня n-ой степени;
• логарифмирование числа;
• возведение в комплексную степень;
• тригонометрические функции комплексных чисел;
• гиперболические функции комплексных чисел;
• взятие комплексно сопряжённого числа;
  • сложение комплексно сопряжённых чисел;
  • вычитание комплексно сопряжённых чисел;
  • умножение комплексно сопряжённых чисел;
  • деление комплексно сопряжённых чисел;
  • обращение комплексно сопряжённого числа.

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970, стр.3б.