Возведение в комплексную степень комплексного числа
Перейти к навигации
Перейти к поиску
Возведение в комплексную степень комплексного числа — это обобщение операции возведения в степень для комплексных чисел .
Формула:
Так как определение опирается на логарифм комплексного числа, который является многозначной аналитической функцией, то и функция возведения в комплексную степень — многозначная.
Обозначения[править]
x1 — действительная часть (абсцисса) первого числа;
y1 — мнимая часть (ордината) первого числа;
x2 — действительная часть (абсцисса) второго числа;
y2 — мнимая часть (ордината) второго числа;
x1 + iy1 — первое комплексное число — основание степени;
x2 + iy2 — второе комплексное число — показатель степени;
lnx — натуральный логарифм вещественного числа;
Ln(x + iy) — комплексный натуральный логарифм.
Формула[править]
Примеры[править]
Другие операции[править]
- сложение чисел;
- вычитание чисел;
- умножение чисел;
- деление чисел;
- обращение числа;
- возведение в степень;
- извлечение квадратного корня;
- извлечение кубического корня;
- извлечение корня n-ой степени;
- логарифмирование числа;
- возведение в комплексную степень;
- тригонометрические функции комплексных чисел;
- гиперболические функции комплексных чисел;
- взятие комплексно сопряжённого числа;
Другие понятия[править]
Литература[править]
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.623.
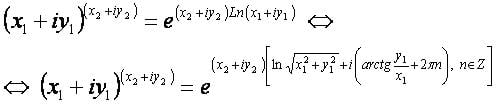
![{\displaystyle (x_{1}+iy_{1})^{(x_{2}+iy_{2})}=e^{(x_{2}+iy_{2})Ln(x_{1}+iy_{1})}=e^{(x_{2}+iy_{2})\left[\ln {\sqrt {x_{1}^{2}+y_{1}^{2}}}+i\left(arctg{\frac {y_{1}}{x_{1}}}+2\pi n\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b7b0b19132efa8bc05b44e62d3e7c21204cd6a5)


![{\displaystyle \Leftrightarrow (x_{1}+iy_{1})^{(x_{2}+iy_{2})}=e^{(x_{2}+iy_{2})\left[\ln {\sqrt {x_{1}^{2}+y_{1}^{2}}}+i\left(arctg{\frac {y_{1}}{x_{1}}}+2\pi n\right)\right]},\ n\in \mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3972a91035130f27a47ffe4c3e0ff96f2dc7eef4)

![{\displaystyle (-x)^{iy}=e^{y\left[(-(2n+1)\pi n+i\ln x)\right]},\ x>0,y\in \mathbb {R} ,\ n\in \mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/59624de4ce0dcc13b17e776b95a7aae17148e69a)











