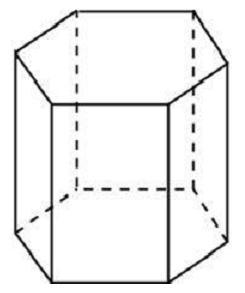
Площадь поверхности правильной призмы

Правильная призма

Геометрия 10 кл Площадь призмы // Образование. Обучение — Znaika TV. Знайка.ру [3:38]

Площадь поверхности правильной призмы — это число, характеризующее правильную призму в единицах измерения площади.

Формула: $S_{\text{прим.п}}=nab+{\frac {na^{2}}{2}}ctg{\frac {\pi }{n}}$, где n — число вершин основания призмы, a — длина стороны основания (ребра), b — длина боковой стороны (ребра) и высота призмы.

Обозначения

Введём обозначения: n — число вершин основания призмы;

(n+2) — число граней призмы (число вершин);

2n — число вершин призмы;

a — длина стороны основания (ребра);

b — длина боковой стороны (ребра) и высота призмы;

P_n — периметр правильного n-угольника;

S_n — площадь основания (правильного n-угольника);

S_бок.n — боковая площадь призмы;

S_призм.n — площадь поверхности правильной призмы.

Формулы

$S_{{\text{призм.}}n}=nab+{\frac {na^{2}}{2}}ctg{\frac {\pi }{n}}\Leftrightarrow$

$\Leftrightarrow S_{{\text{призм.}}n}=S_{{\text{бок.}}n}+2S_{{\text{осн.}}n},\ S_{{\text{бок.}}n}=nab,\ S_{n}={\frac {na^{2}}{4}}ctg{\frac {\pi }{n}}\Leftrightarrow$

$\Leftrightarrow S_{{\text{призм.}}n}=P_{n}\left(b+{\frac {a}{2}}ctg{\frac {\pi }{n}}\right),\ P_{n}=na$

См. также

• Объём правильной призмы
• Площадь поверхности призмы

Площади других многогранников

• призма;
• пирамида;
• усечённая пирамида;
• тетраэдр;
• куб;
• октаэдр;
• додекаэдр;
• икосаэдр;
• правильный n-гранник.