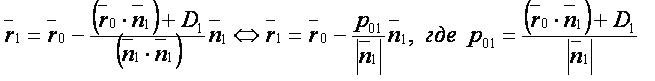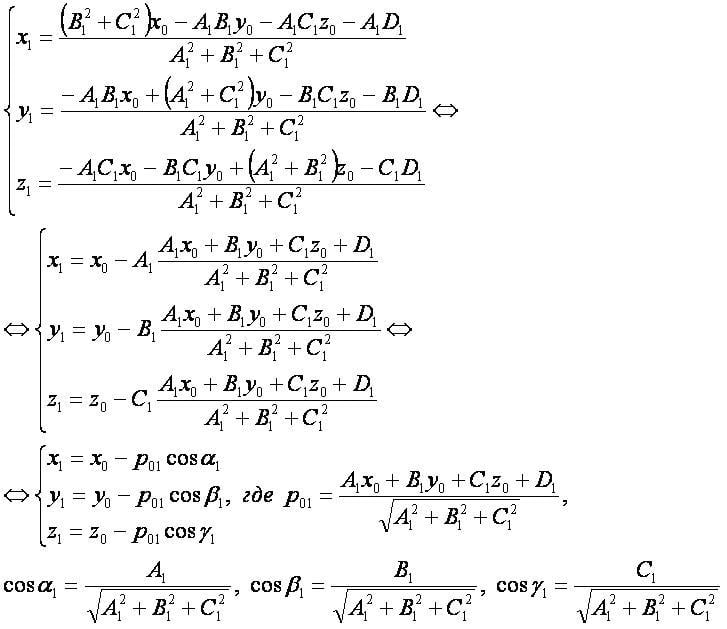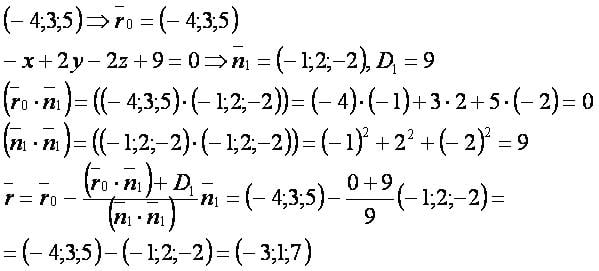Основание перпендикуляра из точки к плоскости в трёхмерном пространстве

Основание перпендикуляра из точки к плоскости — это точка пересечения перпендикуляра и плоскости.

Обозначения

${\bar {r}}_{0}=(x_{0},y_{0},z_{0})$ — радиус-вектор точки;

${\bar {r}}_{1}=(x_{1},y_{1},z_{1})$ — радиус-вектор основания перпендикуляра;

${\bar {n}}_{1}=(A_{1},B_{1},C_{1})$ — нормаль к плоскости;

$A_{1}x+B_{1}y+C_{1}z+D_{1}=0$ — уравнение плоскости;

$p_{01}$ — отклонение точки от плоскости.

Формулы

Векторная форма

Координатная форма

• Заметим, что формулы основания перпендикуляра из точки к плоскости являются частным случаем формул точки пересечения прямой и плоскости, при перпендикулярности прямой к плоскости.

Пример

Даны точка и плоскость: $(-4;3;5)$ и $-x+2y-2z+9=0$.

Найти основание перпендикуляра из точки к плоскости.

Решение.

Другие точки:

1. проекция точки на прямую;
2. проекция точки на плоскость;
3. основание перпендикуляра из точки к прямой;
4. основание перпендикуляра из точки к плоскости;
5. точка пересечения перпендикуляра к двум прямым с первой прямой;
6. точка пересечения перпендикуляра к двум прямым со второй прямой;
7. точка пересечения прямой и плоскости;
8. точка пересечения трёх плоскостей;
9. точка, равноудалённая от двух прямых;
10. точка, равноудалённая от четырёх точек;
11. точка деления отрезка в данном отношении;
12. точка прямой, находящаяся от первой точки прямой до второй в данном отношении;
13. точка прямой, находящаяся перед первой точкой прямой до второй в данном отношении;
14. точка прямой, находящаяся от первой точки прямой за второй в данном отношении.

Ссылки

• Участник:Logic-samara