Аксиоматический метод
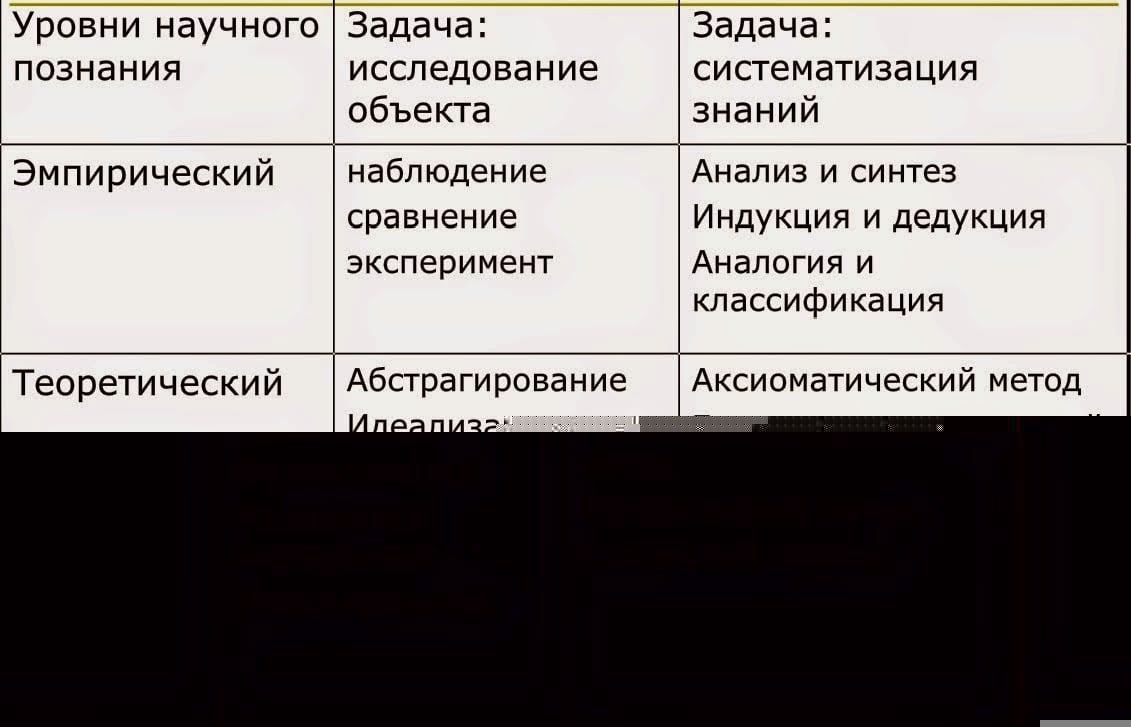
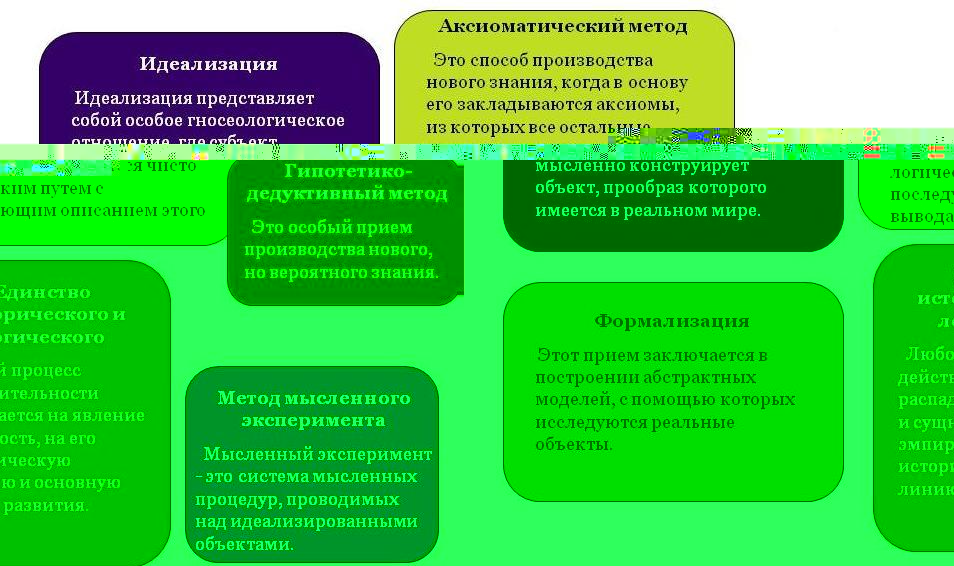
Аксиоматический метод (аксиоматизация науки, аксиоматическое построение научного знания) — способ построения отдельных научных теорий, разделов науки и науки в целом, при котором какие-то положения избираются в качестве исходных и не требующих доказательства (истинных), а все остальные положения выводятся из исходных — доказываются — логическим путём.
Исходные положения, которые принимаются без доказательств, называются аксиомами, а выводимые из аксиом утверждения — теоремами.
Аксиоматический метод изучается в философии науки.
Исторически аксиоматический метод применялся в Древней Греции в труде Евклида «Начала», написанном в 330−320 годах до нашей эры. Впоследствии на аксиоматическом методе была основана вся математика. Широко применяется аксиоматический метод в физике. Аксиоматический метод так или иначе проявляется в любой научной теории, которую удаётся построить на основе математики: это математизация научного знания.
Объективное условие аксиоматизации[править]
Аксиоматическое построение научной теории предполагает стабильность, определенную устойчивость соответствующей части науки, иначе говоря общепринятость соответствующих представлений. На этой стадии теории можно придать законченность, уточнив ее терминологический аппарат и основные выводы.
Тем не менее, согласно современным представлениям о развитии науки, все области науки время от времени испытывают потрясения, которые называются научными революциями или сменами парадигм. В итоге, в процессе развития любой отрасли науки выделяются отрезки спокойного развития, а также отрезки взрывообразного развития, связанного с пересмотром её основ. Данная концепция развития науки была введена в книге Т. Куна «Структура научных революций».
Аксиоматизация научных знаний может произойти только в период спокойного развития («нормальной науки» в терминологии Куна), а не в период смены парадигм соответствующего раздела науки.
Этапы становления аксиоматического метода[править]
Выделяемые в философии науки этапы становления аксиоматического метода тесно связаны с развитием понимания понятия аксиомы.
Выделяют три периода, в которые аксиомы понимались по-разному. В первый период, начавшийся в Древней Греции, где и было впервые сформулировано определение аксиомы, под аксиомами стали пониматься положения, которые будучи совершенно очевидными, интуитивно ясными для всех, не нуждаются в доказательстве. Подобное понимание аксиом преобладало вплоть до XIX века вплоть до построения неевклидовых геометрий.
После появления работ Лобачевского и Бояи, показавших, что в основание геометрии могут быть положены разные системы аксиом, появилось новое понимание аксиомы. Аксиомы стали трактоваться как такие положения теории, которые при данном ее построении как дедуктивной теории принимаются за исходные независимо от того, насколько они просты и интуитивно очевидны. При таком подходе аксиомы перестают носить характер абсолютных истин, а становятся зависимыми от того, какая теория строится на их основе.
Третий этап, идущий с конца XIX — начала XX века, связан с программой формалистического обоснованя математики, появившейся в работах Д. Гильберта и его последователей, которые стали придавать аксиомам строго формальный характер. Аксиомами становятся даже не предложения содержательной теории, а наборы формул, из которых по формально определенным правилам вывода, выводятся другие формулы теории, которая становится, таким образом, исчислением формул.
С учетом перечисленных этапов понимания аксиомы, выделяют три периода становления аксиоматического метода:
- содержательная аксиоматизация
- полуформальная аксиоматизация
- формальная аксиоматизация.
Эти три этапа соответствуют кризисам в математике, связанных с пересмотром ее парадигмы. Иногда первые два этапа рассматриваются как один (так предлагал, например, С. П. Новиков в книге «Элементы математической логики»).
Аксиоматизация как завершение математизации[править]
Существуют прогнозы, что в ходе дальнейшей математизации науки роль аксиоматического метода будет возрастать, а объем аксиоматизированных знаний — увеличиваться.
По В. Я. Перминову, полная математизация теории — это момент ее развития, когда она может быть полностью аксиоматически построена. Полностью математизированная теория консервируется в своих исходных принципах и ее дальнейшее развитие за счет увеличения области приложения и развития математических средств. Консервация теории говорит об ограничении аспекта исследования через саму форму теории и делает необходимым появления более общих теорий, расширяющих предмет исследования.
Полная математизация некоторых теорий, по-видимому, достигнута лишь в физике. В. Я. Перминов делает вывод, что полная математизация всего знания невозможна, что не противоречит тому, что отдельные области научного знания приобретут законченную математическую форму.
Пример попытки аксиоматизации гуманитарного знания: Аксиоматическая теория потребностей.
См. также[править]
Литература[править]
- Акчурин И. А. Место математики в системе наук // «Вопросы философии», 1967, № 1.
- Беляев Е. А., Киселева Н. А., Перминов В. Я. Некоторые особенности математического знания — М.: Издательство Московского университета, 1975. Глава V. Структура и этапы математизации научного знания.
- Александров И. Ю. КРИЗИС КОНЦЕПЦИИ ФУНДАМЕНТАЛИЗМА В ЭПИСТЕМОЛОГИИ И ФОРМИРОВАНИЕ КОНЦЕПЦИИ ПОСТНЕКЛАССИЧЕСКОЙ НАУКИ // Вестник Санкт-Петербургского государственного университета культуры и искусств, Выпуск № 1, 2011.