Площадь поверхности шарового слоя

Шаровой слой

Формула

Площадь поверхности шарового слоя — это сумма боковой площади шарового слоя и площадей оснований шарового слоя.

Под шаровым слоем будем подразумевать часть шара, ограниченную двумя параллельными плоскостями (кругами).

Обозначения

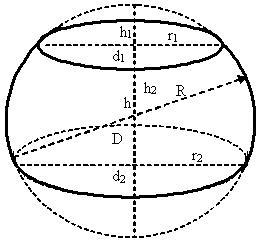
R — радиус шара;

r₁ — радиус верхнего основания шарового слоя и меньшего шарового сегмента;

r₂ — радиус нижнего основания шарового слоя и большего шарового сегмента;

h — высота шарового слоя;

h₁ — высота меньшего шарового сегмента;

h₂ — высота большего шарового сегмента;

S_{бок.шар.слой} — площадь боковой поверхности шарового слоя;

S_{осн.r1сегм} — площадь основания меньшего шарового сегмента;

S_{осн.r2сегм} — площадь основания большего шарового сегмента;

S_{шар.слой} — площадь поверхности шарового слоя.

Формула

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle S_\text{шар.слой}=\pi\left(r_1^2+r_2^2+2Rh\right), \ h=h_2-h_1 \Leftrightarrow}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Leftrightarrow S_\text{шар.слой}=S_\text{бок}+S_{r_1\text{осн}}+S_{r_2\text{осн}}, \ S_\text{бок}=2\pi Rh, \ S_{r_1\text{осн}}=\pi r_1^2, \ S_{r_2\text{осн}}=\pi r_2^2}

• Заметим, что площадь боковой поверхности шарового слоя зависит от высоты слоя и радиуса шара и не зависит от радиусов оснований слоя. Соответственно, площадь боковой поверхности шарового слоя определённой высоты равна площади боковой поверхности шарового сегмента такой же высоты и радиуса шара.

Вывод формулы

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle S_\text{бок.шар.слой}=2\pi\int\limits_{R-h_2}^{R-h_1}\sqrt{R^2-x^2}\sqrt{1+\left(\sqrt{R^2-x^2}'\right)^2}dx=}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle =2\pi\int\limits_{R-h_2}^{R-h_1}\sqrt{R^2-x^2}\sqrt{1+\left(\frac{-x}{\sqrt{R^2-x^2}}\right)^2}dx=2\pi\int\limits_{R-h_2}^{R-h_1}Rdx=2\pi R\int\limits_{R-h_2}^{R-h_1}1dx=}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle =\left.2\pi Rx\right|_{R-h_2}^{R-h_1}=2\pi R(h_2-h_1)=2\pi Rh \Rightarrow S_\text{бок.шар.слой}=2\pi Rh}

См. также

• Объём шарового слоя

Другие формулы

1. фигура вращения;
2. шар;
3. цилиндр;
4. конус;
5. усечённый цилиндр;
6. усечённый конус;
7. шаровой сегмент;
8. шаровой сектор;
9. шаровой слой;
10. шаровой клин;
11. центральный шаровой клин;
12. торовый клин;
13. цилиндрическая труба;
14. цилиндрическое копыто;
15. конусное копыто;
16. шаровое копыто;
17. шаровая бочка;
18. круговая бочка;
19. сегментное кольцо;
20. тор;
21. кокон;
22. купол;
23. сфероид;
24. параболоид вращения.

Литература

• Бронштейн И. Н., Семендяев К. А., Справочник по математике — М., 1956, стр.177.