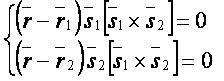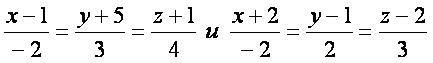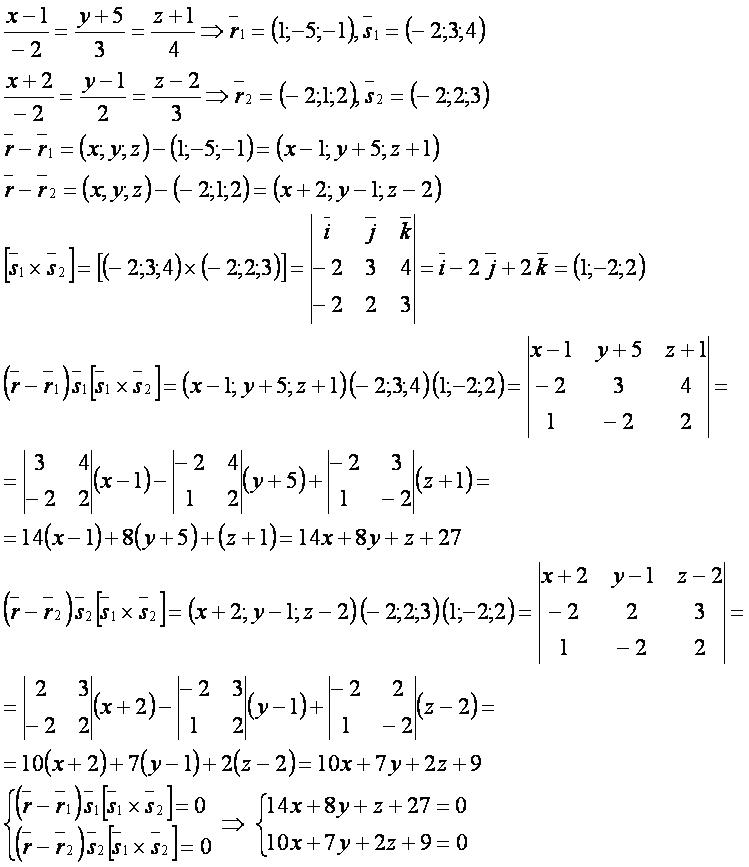Уравнение перпендикуляра к двум прямым

Уравнение перпендикуляра к двум прямым — это уравнение прямой, перпендикулярной к каждой из прямых, задаётся системой равенств нулю смешанных произведений соответствующего вектора-разности радиусов-векторов точек, направляющего вектора и векторного произведения направляющих векторов.

Обозначения

${\bar {r}}=(x,y,z)$ — радиус-вектор точки перпендикуляра;

${\bar {r}}_{1}=(x_{1},y_{1},z_{1})$ — радиус-вектор точки первой прямой;

${\bar {r}}_{2}=(x_{2},y_{2},z_{2})$ — радиус-вектор точки второй прямой;

${\bar {s}}_{1}=(l_{1},m_{1},n_{1})$ — направляющий вектор первой прямой;

${\bar {s}}_{2}=(l_{2},m_{2},n_{2})$ — направляющий вектор второй прямой;

${\frac {x-x_{1}}{l_{1}}}={\frac {y-y_{1}}{m_{1}}}={\frac {z-z_{1}}{n_{1}}}$ — уравнение первой прямой;

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {x-x_{2}}{l_{2}}}={\frac {y-y_{2}}{m_{2}}}={\frac {z-z_{2}}{n_{2}}}}  — уравнение второй прямой.

Уравнения прямой

Векторная форма

Координатная форма

• Заметим, что формулы верны только для скрещивающихся прямых.

Пример

Даны две прямые:

Найти уравнение перпендикуляра к этим прямым.

Решение.

Другие уравнения:

1. общее;
2. каноническое;
3. параметрическое;
4. проходящей через две точки;
5. равноудалённой от трёх точек;
6. проходящей через точку в направлении вектора;
7. проходящей через точку параллельно прямой;
8. проходящей через точку перпендикулярно плоскости;
9. образованной пересечением двух плоскостей;
10. проекции прямой на плоскость;
11. перпендикуляра из точки к прямой;
12. перпендикуляра из точки к плоскости;
13. перпендикуляра к двум прямым.

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.
• Выгодский М. Я. Справочник по высшей математике — М.: Наука, 1964, стр.192.

Ссылки

• Участник:Logic-samara