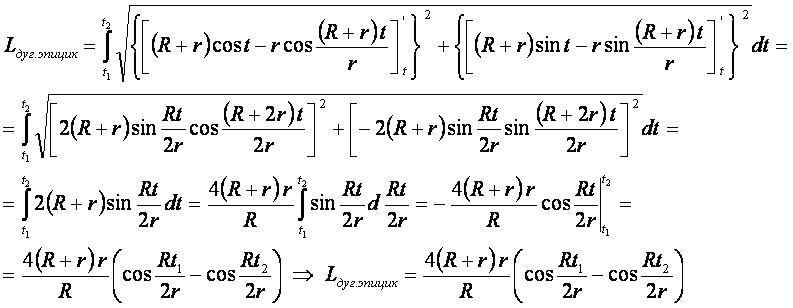Длина дуги эпициклоиды

Формула

Длина дуги эпициклоиды — это число, характеризующее протяжённость дуги эпициклоиды в единицах измерения длины.

Эпициклоида — это линия, описываемая точкой окружности (производящая), когда последняя катится без скольжения по (вне) неподвижной окружности (направляющая).

Рассмотрим дуги эпициклоиды при 0 ≤ t ≤ 2π.

Обозначения

Введём обозначения:

x₁ — абсцисса первой точки дуги;

y₁ — ордината первой точки дуги;

t₁ — параметр (меньший) первой точки дуги;

x₂ — абсцисса второй точки дуги;

y₂ — ордината второй точки дуги;

t₂ — параметр (больший) второй точки дуги;

R — радиус направляющей окружности;

r — радиус производящей окружности;

t — параметрическая переменная;

x = (R + r)cost − rcos[(R + r)t/r] — параметрическое уравнение абсциссы эпициклоиды;

y = (R + r)sint − rsin[(R + r)t/r] — параметрическое уравнение ординаты эпициклоиды;

L_{дуг.эпицик} — длина дуги эпициклоиды.

Формула

$L_{\text{эпицикл}}={\frac {4(R+r)r}{R}}\left(\cos {\frac {Rt_{1}}{2r}}-\cos {\frac {Rt_{2}}{2r}}\right),\ 0\leq t_{1}\leq t_{2}\leq {\frac {\pi r}{R}}$

• Заметим, что кардиоида является эпициклоидой.

Вывод формулы

• Для вывода используется формула длина дуги плоской кривой для функции, заданной параметрически.

Другие формулы

• плоская кривая;
• окружность;
• парабола;
• эллипс;
• гипербола;
• синусоида;
• косинусоида;
• циклоида;
• кардиоида;
• астроида;
• эпициклоида;
• гипоциклоида;
• эвольвента;
• цепная линия;
• трактриса;
• лемниската Бернулли.

Ссылки

• Выгодский М. Я. Справочник по высшей математике. М.: Наука, 1964, стр.805.
• Участник:Logic-samara