Длина дуги цепной линии

Цепная линия

Формула

Длина дуги цепной линии — это число, характеризующее протяжённость дуги цепной линии в единицах измерения длины.

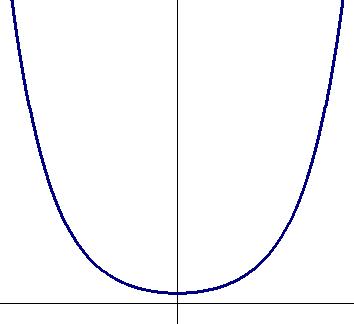
Цепная линия (висящая цепь) — это линия, образуемая гибкой тяжёлой нерастяжимой нитью (цепью), подвешенной в двух точках. График цепной линии имеет вид графика гиперболического косинуса.

Рассмотрим дуги цепной линии, с вершиной в точке (0, R).

Обозначения

Введём обозначения:

x₁ — абсцисса (меньшая) первой точки;

y₁ — ордината первой точки;

x₂ — абсцисса (большая) второй точки;

y₂ — ордината второй точки;

R — ордината вершины цепной линии;

M = (x, y) — точка цепной линии;

M₀ = (0, R) — вершина цепной линии;

y = Rch(x/R) — уравнение цепной линии;

L_{дуг.цеп} — длина дуги цепной линии.

Формула

$L_{\text{дуг.цеп}}=R\left(sh{\frac {x_{2}}{R}}-sh{\frac {x_{1}}{R}}\right)\Leftrightarrow L_{\text{дуг.цеп}}={\frac {1}{2}}R\left(e^{\frac {x_{2}}{R}}-e^{-{\frac {x_{2}}{R}}}-e^{\frac {x_{1}}{R}}+e^{-{\frac {x_{1}}{R}}}\right)$

• Длина дуги цепной линии M₀M от вершины равна L_x = Rsh(x/R).

Вывод формулы

$L_{\text{дуг.цеп}}=\int \limits _{x_{1}}^{x_{2}}{\sqrt {1+\left(y'_{x}(x)\right)^{2}}}dx=\int \limits _{x_{1}}^{x_{2}}{\sqrt {1+\left[\left(Rch{\frac {x}{R}}\right)'_{x}\right]^{2}}}dx=\int \limits _{x_{1}}^{x_{2}}{\sqrt {1+\left(sh{\frac {x}{R}}\right)^{2}}}dx=$

$=\int \limits _{x_{1}}^{x_{2}}{\sqrt {1+sh^{2}{\frac {x}{R}}}}dx=\int \limits _{x_{1}}^{x_{2}}{\sqrt {ch^{2}{\frac {x}{R}}}}dx=\int \limits _{x_{1}}^{x_{2}}ch{\frac {x}{R}}dx=R\int \limits _{x_{1}}^{x_{2}}ch{\frac {x}{R}}d{\frac {x}{R}}=\left.Rsh{\frac {x}{R}}\right|_{x_{1}}^{x_{2}}=$

$=R\left(sh{\frac {x_{2}}{R}}-sh{\frac {x_{1}}{R}}\right)\Rightarrow L_{\text{дуг.цеп}}=R\left(sh{\frac {x_{2}}{R}}-sh{\frac {x_{1}}{R}}\right)$

• Для вывода используется формула «длина дуги плоской кривой» в прямоугольных координатах.

См. также

• Площадь, ограниченная цепной линией и осью абсцисс

Другие формулы

• плоская кривая;
• окружность;
• парабола;
• эллипс;
• гипербола;
• синусоида;
• косинусоида;
• циклоида;
• кардиоида;
• астроида;
• эпициклоида;
• гипоциклоида;
• эвольвента;
• цепная линия;
• трактриса;
• лемниската Бернулли.

Литература

• Бронштейн М. Н., Семендяев К. А., Справочник по математике — М., 1956, стр.113.
• Выгодский М. Я. Справочник по высшей математике — М.: Наука, 1964, стр.829.