Длина дуги лемнискаты Бернулли

Лемниската Бернулли

Длина дуги лемнискаты Бернулли — это число, характеризующее протяжённость дуги лемнискаты Бернулли в единицах измерения длины.

Обозначения

Введём обозначения:

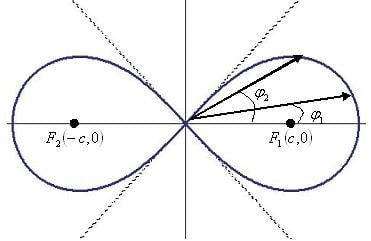
F₁ — правый фокус;

F₂ — левый фокус;

c — половина расстояния между фокусами;

(x² + y²)² = 2c²(x² − y²) — уравнение лемнискаты Бернулли;

φ₁ — угол (меньший) первой точки дуги;

φ₂ — угол (больший) второй точки дуги;

φ — независимая переменная;

r² = 2c²cos2φ — уравнение лемнискаты Бернулли в полярных координатах;

t₁ — параметр первой точки дуги;

t₂ — параметр второй точки дуги;

t — вспомогательная параметричиская переменная;

F(k, t) — эллиптический интеграл I рода;

L_{дуг.лемн} — длина дуги лемнискаты Бернулли.

Формула

[math]\displaystyle{ L_{\text{дуг.лемн}}=cF\left(\frac{\sqrt{2}}{2},\arcsin(\sqrt{2}\sin(\varphi_2))\right)-cF\left(\frac{\sqrt{2}}{2},\arcsin(\sqrt{2}\sin(\varphi_1))\right), \ 0 \le \varphi_1 \le \varphi_2 \le \frac{\pi}{4} }[/math]

• Периметр лемнискаты Бернулли (из двух лепестков) равен P_лемн = 4cF(√2/2, π/2).

Вывод формулы

• Для вывода используется формула «длина дуги плоской кривой» в полярных координатах.
• Для нахождения интеграла используется эллиптический интеграл I рода.

См. также

• Площадь сектора лемнискаты Бернулли

Другие формулы

• длина дуги плоской кривой;
• длина дуги окружности;
• длина дуги параболы;
• длина дуги эллипса;
• длина дуги гиперболы;
• длина дуги синусоиды;
• длина дуги косинусоиды;
• длина дуги циклоиды;
• длина дуги кардиоиды;
• длина дуги астроиды;
• длина дуги эпициклоиды;
• длина дуги гипоциклоиды;
• длина дуги эвольвенты окружности;
• длина дуги цепной линии;
• длина дуги трактрисы;
• длина дуги лемнискаты Бернулли.

Ссылки

• Храбров А. И. Немного об эллиптических интегралах
• Участник:Logic-samara