Площадь сектора лемнискаты Бернулли

Лемниската Бернулли

Формула

Площадь сектора лемнискаты Бернулли — это число, характеризующее сектор лемнискаты Бернулли в единицах измерения площади.

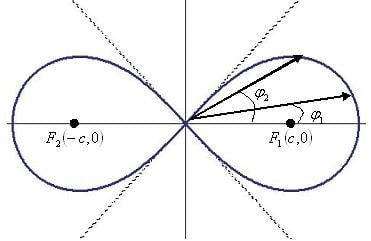
Сектор лемнискаты Бернулли — это часть лемнискаты Бернулли, отсекаемая двумя прямыми (радиусами), проходящими через центр симметрии.

Рассмотрим секторы лемнискаты Бернулли, отсекаемые двумя прямыми, проходящими через центр симметрии в первом квадранте.

Обозначения

Введём обозначения:

F₁ — правый фокус;

F₂ — левый фокус;

c — половина расстояния между фокусами;

(x² + y²)² = 2c²(x² − y²) — уравнение лемнискаты Бернулли;

φ₁ — угол (меньший) первой точки сектора;

φ₂ — угол (больший) второй точки сектора;

φ — независимая переменная;

r² = 2c²cos2φ — уравнение лемнискаты Бернулли в полярных координатах;

S_{сект.лемн} — площадь сектора лемнискаты Бернулли.

Формулы

$S_{\text{сект.лемн}}={\frac {1}{2}}c^{2}(\sin 2\varphi _{2}-\sin 2\varphi _{1}),\ -{\frac {\pi }{4}}\leq \varphi _{1}\leq \varphi _{2}\leq {\frac {\pi }{4}}$

• Площадь лемнискаты Бернулли (из двух лепестков) равна S_лемн = 2с².

Вывод формул

$S_{\text{сект.лемн}}={\frac {1}{2}}\int \limits _{\varphi _{1}}^{\varphi _{2}}r^{2}d\varphi ={\frac {1}{2}}\int \limits _{\varphi _{1}}^{\varphi _{2}}2c^{2}\cos 2\varphi d\varphi ={\frac {1}{2}}c^{2}\int \limits _{\varphi _{1}}^{\varphi _{2}}\cos 2\varphi d2\varphi =$

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle =\left.\frac{1}{2}c^2\sin 2\varphi\right|_{\varphi_1}^{\varphi_2}=\frac{1}{2}c^2(\sin 2\varphi_2-\sin 2\varphi_1) \Rightarrow S_\text{сект.лемн}=\frac{1}{2}c^2(\sin 2\varphi_2-\sin 2\varphi_1)}

• Для вывода используется формула «площадь плоской фигуры» в полярных координатах.

См. также

• Длина дуги лемнискаты Бернулли

Другие формулы

1. треугольник;
2. четырёхугольник;
3. круг;
4. сегмент круга;
5. сектор круга;
6. серп;
7. эллипс;
8. сегмент эллипса;
9. сектор эллипса;
10. серп эллипса;
11. сегмент параболы;
12. сегмент гиперболы;
13. сектор кардиоиды;
14. сектор лемнискаты Бернулли;
15. правильный многоугольник;
16. сегмент правильного многоугольника;
17. сектор правильного многоугольника;
18. арка циклоиды;
19. сектор кардиоиды;
20. сектор лемнискаты Бернулли.
21. арка синусоиды;
22. арка косинусоиды;
23. фигура, ограниченная тангенсоидой и осью абсцисс;
24. фигура, ограниченная котангенсоидой и осью абсцисс;
25. треугольник Рёло;
26. пятиугольник Рёло;
27. многоугольник Рёло;
28. общая плоская фигура.