Площадь сектора эллипса

Сектор, симметричный относительно большой оси эллипса

Сектор, симметричный относительно малой оси эллипса

Площадь сектора эллипса — это число, характеризующее сектор эллипса в единицах измерения площади.

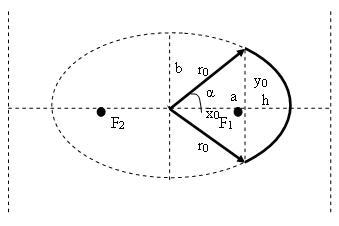
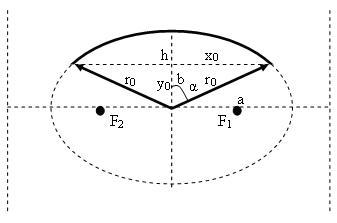
Сектор эллипса — это часть эллипса, отсекаемая двумя прямыми (радиусами), проходящими через центр симметрии.

Рассмотрим (меньшие) секторы эллипса, отсекаемые двумя прямыми, проходящими через центр симметрии и симметричными относительно осей эллипса.

Обозначения

Введём обозначения:

a — большая полуось эллипса;

b — малая полуось эллипса;

h — высота сегмента;

x₀ — абсцисса крайней точки сектора;

y₀ — ордината крайней точки сектора;

r₀ — расстояние (крайний радиус) от центра эллипса до крайней точки сектора;

α — угол между осью симметрии сектора и радиусом крайней точки сектора;

S_{сект.элл} — площадь сектора эллипса.

Формулы

Площадь сектора, симметричного относительно большой оси эллипса

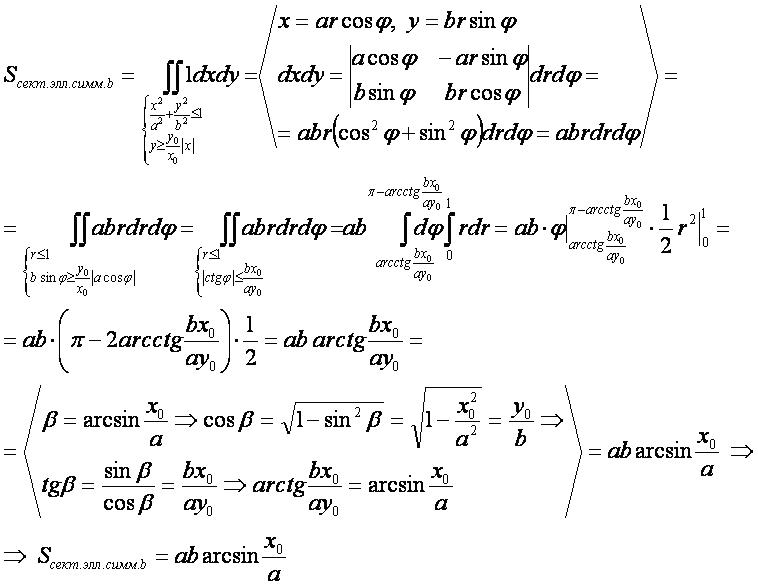
Площадь сектора, симметричного относительно малой оси эллипса

Вывод формул

Площадь сектора, симметричного относительно большой оси эллипса

1-й способ

• Для вывода используется формула «площадь плоской фигуры» в прямоугольных координатах.
• Для нахождения интеграла используется формула 3 «интегралы функций с корнями».

2-й способ

• Для вывода используется формула «площадь плоской фигуры» в прямоугольных координатах.
• Для нахождения интеграла используется «метод замены переменных» и переход к

полярным координатам.

Площадь сектора, симметричного относительно малой оси эллипса

1-й способ

• Для вывода используется формула «площадь плоской фигуры» в прямоугольных координатах.
• Для нахождения интеграла используется формула 3 «интегралы функций с корнями».

2-й способ

• Для вывода используется формула «площадь плоской фигуры» в прямоугольных координатах.
• Для нахождения интеграла используется «метод замены переменных» и переход к

полярным координатам.

Площадь сектора

Рассмотрим секторы эллипса, отсекаемые двумя произвольными прямыми, проходящими через центр симметрии.

Площадь сектора равна алгебраической сумме площадей соответствующих полусекторов (с соответствующим знаком).

См. также

• Длина дуги эллипса

Другие формулы

1. треугольник;
2. четырёхугольник;
3. круг;
4. сегмент круга;
5. сектор круга;
6. серп;
7. эллипс;
8. сегмент эллипса;
9. сектор эллипса;
10. серп эллипса;
11. сегмент параболы;
12. сегмент гиперболы;
13. сектор кардиоиды;
14. сектор лемнискаты Бернулли;
15. правильный многоугольник;
16. сегмент правильного многоугольника;
17. сектор правильного многоугольника;
18. арка циклоиды;
19. сектор кардиоиды;
20. сектор лемнискаты Бернулли.
21. арка синусоиды;
22. арка косинусоиды;
23. фигура, ограниченная тангенсоидой и осью абсцисс;
24. фигура, ограниченная котангенсоидой и осью абсцисс;
25. треугольник Рёло;
26. пятиугольник Рёло;
27. многоугольник Рёло;
28. общая плоская фигура.

Ссылки

• Участник:Logic-samara