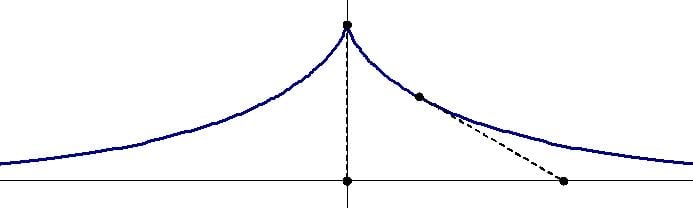
Площадь, ограниченная трактрисой и осью абсцисс

Трактриса

Формула

Площадь, ограниченная трактрисой и осью абсцисс, — это число, характеризующее область под трактрисой при 0 < x < ∞ в единицах измерения площади.

Рассмотрим области трактрисы, исходящей из точки (0, R).

Обозначения

Введём обозначения:

x₁ — абсцисса (большая) первой точки;

y₁ — ордината первой точки;

t₁ — параметр (меньший) первой точки;

x₂ — абсцисса (меньшая) второй точки;

y₂ — ордината второй точки;

t₂ — параметр (больший) второй точки;

R — высота трактрисы;

L — точка оси абсцисс, являющейся направляющей;

M = (x, y) — точка трактрисы;

M₀ = (0, R) — вершина трактрисы;

t — параметрическая переменная;

x = R[cost + lntg(t/2)] — параметрическое уравнение абсциссы трактрисы;

y = Rsint — параметрическое уравнение ординаты трактрисы;

S_трак — площадь, ограниченная дугой трактрисы и осью абсцисс при 0 ≤ x₂ ≤ x₁ < ∞.

Формула

$S_{\text{трак}}={\frac {1}{4}}R^{2}(2t_{2}+\sin 2t_{2}-2t_{1}-\sin 2t_{1}),\ 0<t_{1}\leq t_{2}\leq {\frac {\pi }{2}}$

• Площадь, ограниченная дугой трактрисы M₀M и осью абсцисс, равна S_t = R²(π − 2t − sin2t)/4.
• Площадь, ограниченная трактрисой и осью абсцисс, равна половине площади круга радиуса равного высоте, S_трак = πR²/2.

Вывод формулы

$S_{\text{трак}}=\int \limits _{t_{1}}^{t_{2}}R\sin t\left(R\cos t+R\ln tg{\frac {t}{2}}\right)'_{t}dt=\int \limits _{t_{1}}^{t_{2}}R\sin t\left(-R\sin t+{\frac {R}{\sin t}}\right)dt=$

$=R^{2}\int \limits _{t_{1}}^{t_{2}}(-sin^{2}t+1)dt=R^{2}\int \limits _{t_{1}}^{t_{2}}\cos ^{2}tdt=R^{2}\int \limits _{t_{1}}^{t_{2}}{\frac {1+\cos 2t}{2}}dt=\left.{\frac {1}{4}}R^{2}(2t+\sin 2t)\right|_{t_{1}}^{t_{2}}=$

$={\frac {1}{4}}R^{2}(2t_{2}+\sin 2t_{2}-2t_{1}-\sin 2t_{1})\Rightarrow S_{\text{трак}}={\frac {1}{4}}R^{2}(2t_{2}+\sin 2t_{2}-2t_{1}-\sin 2t_{1})$

• Для вывода используется формула «площадь плоской фигуры» в параметрической форме.

См. также

• Длина дуги трактрисы

Другие формулы

• плоская фигура;
• круг;
• сегмент круга;
• сектор круга;
• сегмент правильного многоугольника;
• сектор правильного многоугольника;
• серп;
• сегмент параболы;
• эллипс;
• сегмент эллипса;
• сектор эллипса;
• серп эллипса;
• сегмент гиперболы;
• арка синусоиды;
• арка косинусоиды;
• фигура, ограниченная тангенсоидой и осью абсцисс;
• фигура, ограниченная котангенсоидой и осью абсцисс;
• арка циклоиды;
• сектор кардиоиды;
• фигура, ограниченная цепной линией и осью абсцисс;
• фигура, ограниченная трактрисой и осью абсцисс;
• сектор лемнискаты Бернулли.