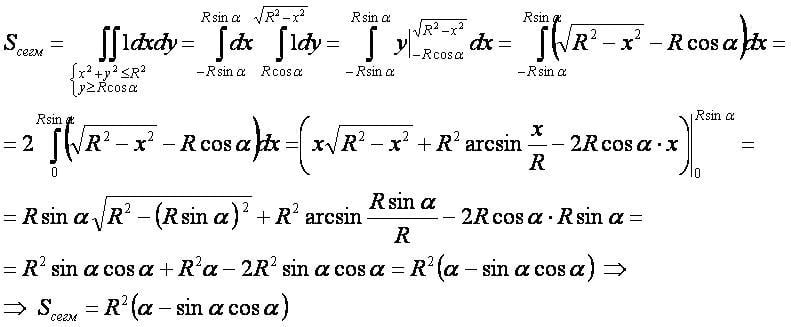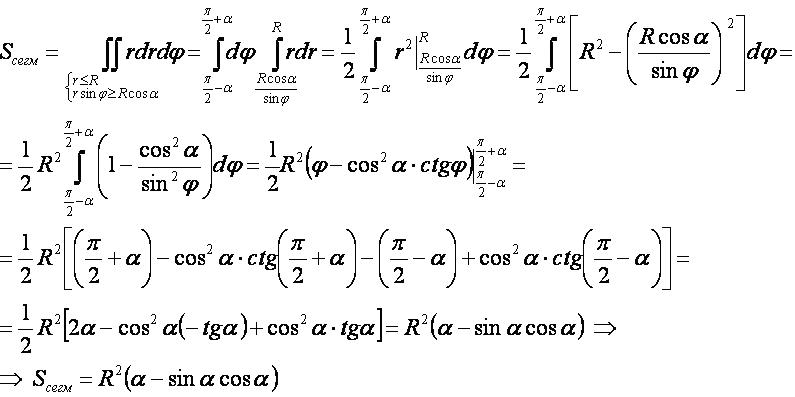Площадь сегмента круга

Сегмент круга с α<π/2

Сегмент круга с α>π/2

Площадь сегмента круга — это число, характеризующее сегмент круга в единицах измерения площади.

Сегмент круга — это часть круга, отсекаемая прямой.

Обозначения

Введём обозначения:

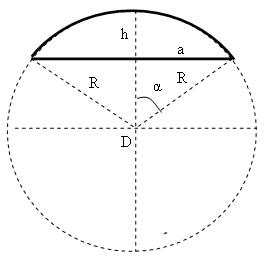
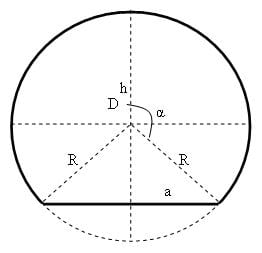
R — радиус круга;

a — полуоснование сегмента;

h — высота сегмента;

R-h — отклонение основания сегмента от центра круга;

α — угол между осью симметрии сегмента и радиусом в крайней точке сегмента;

S_сегм — площадь сегмента круга.

Формула

$S_{\text{сегм}}=R^{2}(\alpha -\sin \alpha \cos \alpha )\Leftrightarrow$

$S_{\text{сегм}}=R(R\alpha -a\cos \alpha ),\ a=R\sin \alpha \Leftrightarrow$

$S_{\text{сегм}}=R^{2}\alpha -a(R-h),\ h=R(1-\cos \alpha )\Leftrightarrow$

$S_{\text{сегм}}=R^{2}\alpha -asign(R-h){\sqrt {R^{2}-a^{2}}},\ h=R-sign(R-h){\sqrt {R^{2}-a^{2}}}\Leftrightarrow$

$S_{\text{сегм}}={\frac {1}{4}}D^{2}(\alpha -\sin \alpha \cos \alpha ),\ D=2R$

Вывод формулы

1-й способ

• Для вывода используется формула «площадь плоской фигуры» в прямоугольных координатах.
• Для нахождения интеграла используется формула 3 «интегралы функций с корнями».

2-й способ

• Для вывода используется формула «площадь плоской фигуры» в полярных координатах.

См. также

• Длина дуги окружности

Другие формулы

• плоская фигура;
• круг;
• сегмент круга;
• сектор круга;
• сегмент правильного многоугольника;
• сектор правильного многоугольника;
• серп;
• сегмент параболы;
• эллипс;
• сегмент эллипса;
• сектор эллипса;
• серп эллипса;
• сегмент гиперболы;
• арка синусоиды;
• арка косинусоиды;
• фигура, ограниченная тангенсоидой и осью абсцисс;
• фигура, ограниченная котангенсоидой и осью абсцисс;
• арка циклоиды;
• сектор кардиоиды;
• фигура, ограниченная цепной линией и осью абсцисс;
• фигура, ограниченная трактрисой и осью абсцисс;
• сектор лемнискаты Бернулли.

Ссылки

• Участник:Logic-samara