Длина дуги трактрисы

Трактриса

Длина дуги трактрисы — это число, характеризующее протяжённость дуги трактрисы в единицах измерения длины.

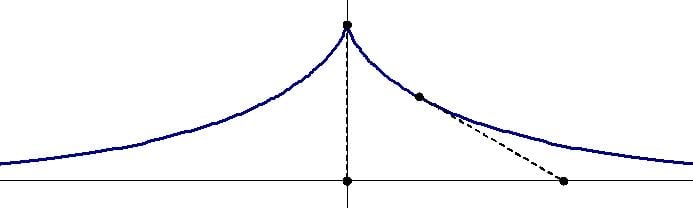
Трактриса — это линия, исходящая из вершины M₀ в обе стороны, описываемая точкой M, увлекаемой нерастяжимой нитью LM длиной R, при движении точки L по направляющей (оси абсцисс).

Рассмотрим дуги трактрисы, исходящей из точки (0, R).

Обозначения

Введём обозначения:

x₁ — абсцисса (меньшая) первой точки;

y₁ — ордината первой точки;

t₁ — параметр (меньший) первой точки;

x₂ — абсцисса (большая) второй точки;

y₂ — ордината второй точки;

t₂ — параметр (больший) второй точки;

R — высота трактрисы;

L — точка оси абсцисс, являющейся направляющей;

M = (x, y) — точка трактрисы;

M₀ = (0, R) — вершина трактрисы;

t — параметрическая переменная (угол наклона трактрисы);

x = R[cost + lntg(t/2)] — параметрическое уравнение абсциссы трактрисы;

y= Rsint — параметрическое уравнение ординаты трактрисы;

L_{дуг.трак} — длина дуги трактрисы.

Формула

[math]\displaystyle{ L_{\text{дуг.трак}}=R\ln\left|\frac{\sin t_1}{\sin t_2}\right|, \ \frac{\pi}{2}\le t_1 \le t_2 \lt \pi }[/math]

• Длина дуги трактрисы M₀M от вершины равна L_t = −Rln|sint|.

Вывод формулы

[math]\displaystyle{ L_\text{дуг.трак}=\int\limits_{t_1}^{t_2}\sqrt{\left(x_t'\right)^2+\left(y_t'\right)^2}dt=\int\limits_{t_1}^{t_2}\sqrt{\left[\left(R\cos t+R\ln tg\frac{t}{2}\right)'_t\right]^2+\left[(R\sin t)'_t\right]^2}dt= }[/math]

[math]\displaystyle{ =\int\limits_{t_1}^{t_2}\sqrt{\left(-R\sin t+\frac{R}{\sin t}\right)^2+(R\cos t)^2}dt=R\int\limits_{t_1}^{t_2}\sqrt{\sin^2t-2+\frac{1}{\sin^2t}+\cos^2t}dt= }[/math]

[math]\displaystyle{ =R\int\limits_{t_1}^{t_2}\sqrt{\frac{1}{\sin^2t}-1}dt=R\int\limits_{t_1}^{t_2}\sqrt{\frac{1-\sin^2t}{\sin^2t}}dt=R\int\limits_{t_1}^{t_2}\sqrt{\frac{\cos^2t}{\sin^2t}}dt=R\int\limits_{t_1}^{t_2}\frac{-\cos t}{\sin t}dt= }[/math]

[math]\displaystyle{ =-R\int\limits_{t_1}^{t_2}\frac{1}{\sin t}d\sin t=\left.-R\ln|\sin t|\right|_{t_1}^{t_2}=-R(\ln|\sin t_2|-\ln|\sin t_1|)=R\ln\left|\frac{\sin t_1}{\sin t_2}\right| \Rightarrow }[/math]

[math]\displaystyle{ \Rightarrow L_\text{дуг.трак}=R\ln\left|\frac{\sin t_1}{\sin t_2}\right| }[/math]

• Для вывода используется формула «длина дуги плоской кривой» в параметрической форме.

См. также

• Площадь, ограниченная трактрисой и осью абсцисс

Другие формулы

• длина дуги плоской кривой;
• длина дуги окружности;
• длина дуги параболы;
• длина дуги эллипса;
• длина дуги гиперболы;
• длина дуги синусоиды;
• длина дуги косинусоиды;
• длина дуги циклоиды;
• длина дуги кардиоиды;
• длина дуги астроиды;
• длина дуги эпициклоиды;
• длина дуги гипоциклоиды;
• длина дуги эвольвенты окружности;
• длина дуги цепной линии;
• длина дуги трактрисы;
• длина дуги лемнискаты Бернулли.

Литература

• Бронштейн М. Н., Семендяев К. А., Справочник по математике — М., 1956, стр.114.
• Выгодский М. Я. Справочник по высшей математике — М.: «Наука», 1964, стр.822.