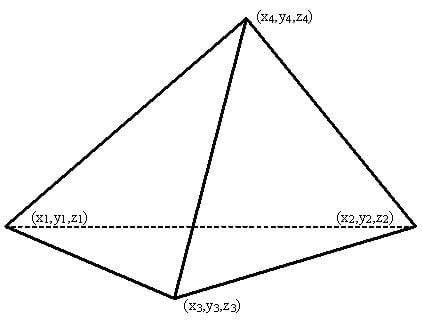
Площадь поверхности правильного тетраэдра

Тетраэдр

Площадь поверхности правильного тетраэдра — это число, характеризующее правильный тетраэдр в единицах измерения площади.

Обозначения

Введём обозначения:

a — длина ребра;

h — высота;

r — радиус вписанной сферы;

R — радиус описанной сферы;

S_треуг — площадь правильного треугольника (грани);

V_тетр — объём тетраэдра;

S_тетр — площадь поверхности тетраэдра.

Формула

$S_{\text{тетр}}={\sqrt {3}}a^{2}\Leftrightarrow S_{\text{тетр}}=4S_{\text{треуг}},\ S_{\text{треуг}}={\frac {\sqrt {3}}{4}}a^{2}\Leftrightarrow$

$S_{\text{тетр}}={\frac {3V_{\text{тетр}}}{r}},\ V_{\text{тетр}}={\frac {\sqrt {2}}{12}}a^{3},\ r={\frac {\sqrt {6}}{12}}a\Leftrightarrow$

$S_{\text{тетр}}={\frac {8{\sqrt {3}}}{3}}R^{2},\ R={\frac {\sqrt {6}}{4}}a\Leftrightarrow S_{\text{тетр}}=24{\sqrt {3}}r^{2},\ r={\frac {1}{3}}R$

Площадь других многогранников

• призма;
• пирамида;
• усечённая пирамида;
• тетраэдр;
• куб;
• октаэдр;
• додекаэдр;
• икосаэдр;
• правильный n-гранник.

Другие формулы:

• площадь многоугольника;
• площадь правильного многоугольника;
• площадь криволинейного многоугольника;
• площадь плоской фигуры;
• площадь многогранника;
• площадь правильного многогранника;
• площадь поверхности;
• площадь поверхности фигуры вращения.