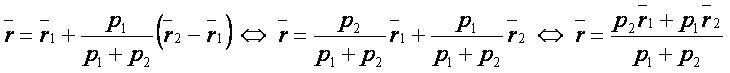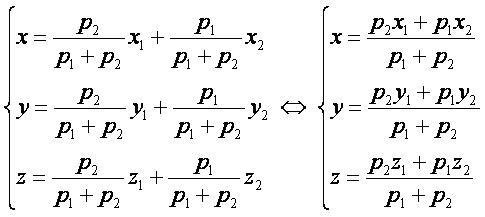Точка деления отрезка в данном отношении в трёхмерном пространстве
Перейти к навигации
Перейти к поиску
Точка деления отрезка в данном отношении — это точка между концами отрезка.
Обозначения[править]
— радиус-вектор точки деления отрезка;
— радиус-вектор первой точки отрезка;
— радиус-вектор второй точки отрезка;
— отношение частей отрезка.
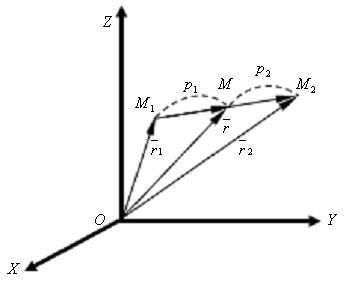
Рисунок[править]
Формулы:[править]
Векторная форма:[править]
Координатная форма:[править]
- Заметим, что формулы точки деления отрезка в данном отношении аналогичны формулам точки прямой, находящейся от первой точки прямой до второй в данном отношении.
Другие точки:[править]
- проекция точки на прямую;
- проекция точки на плоскость;
- основание перпендикуляра из точки к прямой;
- основание перпендикуляра из точки к плоскости;
- точка пересечения перпендикуляра к двум прямым с первой прямой;
- точка пересечения перпендикуляра к двум прямым со второй прямой;
- точка пересечения прямой и плоскости;
- точка пересечения трёх плоскостей;
- точка, равноудалённая от двух прямых;
- точка, равноудалённая от четырёх точек;
- точка деления отрезка в данном отношении;
- точка прямой, находящаяся от первой точки прямой до второй в данном отношении;
- точка прямой, находящаяся перед первой точкой прямой до второй в данном отношении;
- точка прямой, находящаяся от первой точки прямой за второй в данном отношении.
Ссылки[править]
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Выгодский М. Я. Справочник по высшей математике. М.: Наука, 1964, стр.135.
- Бронштейн М. Н., Семендяев К. А., Справочник по математике. М., 1956, стр.219.
- Участник:Logic-samara