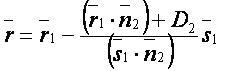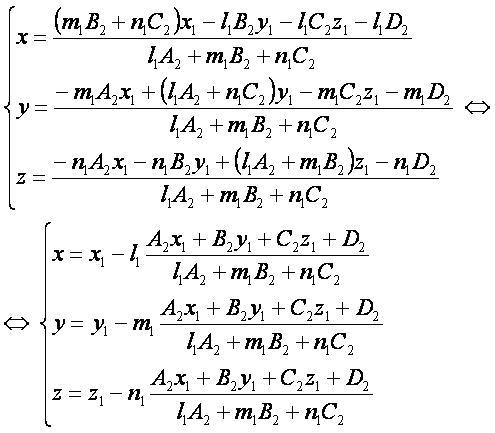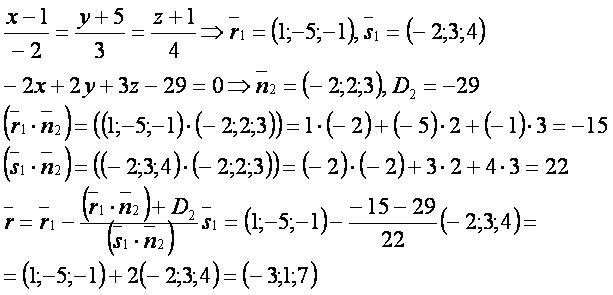Точка пересечения прямой и плоскости

Точка пересечения прямой и плоскости — это точка, удовлетворяющая уравнениям прямой и плоскости.

Обозначения

${\bar {r}}_{1}=(x_{1},y_{1},z_{1})$ — радиус-вектор точки прямой;

${\bar {r}}_{2}=(x_{2},y_{2},z_{2})$ — радиус-вектор точки пересечения прямой и плоскости;

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {s}}_{1}=(l_{1},m_{1},n_{1})}  — направляющий вектор прямой;

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {n}}_{2}=(A_{2},B_{2},C_{2})}  — нормаль к плоскости;

${\frac {x-x_{1}}{l_{1}}}={\frac {y-y_{1}}{m_{1}}}={\frac {z-z_{1}}{n_{1}}}$ — уравнение прямой;

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle A_{2}x+B_{2}y+C_{2}z+D_{2}=0}  — уравнение плоскости.

Формулы

Векторная форма

Координатная форма

• Заметим, что при перпендикулярности прямой к плоскости формулы точки пересечения прямой и плоскости совпадают с формулами основания перпендикуляра из точки к плоскости.
• Заметим, что для определения координат точки пересечения прямой и плоскости достаточно, записав уравнения прямой и плоскости в систему, решить систему методами линейной алгебры.

Пример

Даны прямая и плоскость: ${\frac {x-1}{-2}}={\frac {y+5}{3}}={\frac {z+1}{4}}$ и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle -2x+2y+3z-29=0} .

Найти точку пересечения прямой и плоскости.

Решение.

Другие точки:

1. проекция точки на прямую;
2. проекция точки на плоскость;
3. основание перпендикуляра из точки к прямой;
4. основание перпендикуляра из точки к плоскости;
5. точка пересечения перпендикуляра к двум прямым с первой прямой;
6. точка пересечения перпендикуляра к двум прямым со второй прямой;
7. точка пересечения прямой и плоскости;
8. точка пересечения трёх плоскостей;
9. точка, равноудалённая от двух прямых;
10. точка, равноудалённая от четырёх точек;
11. точка деления отрезка в данном отношении;
12. точка прямой, находящаяся от первой точки прямой до второй в данном отношении;
13. точка прямой, находящаяся перед первой точкой прямой до второй в данном отношении;
14. точка прямой, находящаяся от первой точки прямой за второй в данном отношении.

Ссылки

• Участник:Logic-samara