Длина дуги кардиоиды

Формула

Кардиоида

Длина дуги кардиоиды — это число, характеризующее протяжённость дуги кардиоиды в единицах измерения длины.

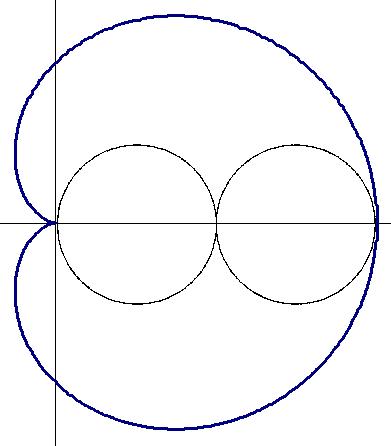
Кардиоида — это линия, описываемая точкой окружности, когда последняя катится без скольжения по окружности того же радиуса.

Катящаяся окружность называется производящей.

Рассмотрим дуги кардиоиды при -π ≤ φ ≤ π.

Обозначения

Введём обозначения:

x₁ — абсцисса первой точки дуги;

y₁ — ордината первой точки дуги;

φ₁ — угол (меньший) первой точки дуги;

x₂ — абсцисса второй точки дуги;

y₂ — ордината второй точки дуги;

φ₂ — угол (больший) второй точки дуги;

R — радиус производящей окружности;

φ — независимая переменная;

r = 2R(1 + cosφ) — уравнение кардиоиды в полярных координатах;

t — параметрическая переменная;

x = 2Rcost(1 + cost) — параметрическое уравнение абсциссы кардиоиды;

y = 2Rsint(1 + cost) — параметрическое уравнение ординаты кардиоиды;

L_{дуг.кард} — длина дуги кардиоиды.

Формула

[math]\displaystyle{ L_\text{дуг.кард}=8R\left(\sin\frac{\varphi_2}{2}-\sin\frac{\varphi_1}{2}\right), \ -\pi \le \varphi_1 \le \varphi_2 \le \pi }[/math]

• Длина полной (от -π до π) кардиоиды равна шестнадцати радиусам производящей окружности, L_кард = 16R.

Вывод формулы

[math]\displaystyle{ L_\text{дуг.кард}=\int\limits_{\varphi_1}^{\varphi_2}\sqrt{r^2+\left(r'_\varphi\right)^2}d\varphi=\int\limits_{\varphi_1}^{\varphi_2}\sqrt{\left(2R\cos\varphi+2R\right)^2+\left[\left(2R\cos\varphi+2R\right)'_\varphi\right]^2}d\varphi= }[/math]

[math]\displaystyle{ =\int\limits_{\varphi_1}^{\varphi_2}\sqrt{4R^2(\cos\varphi+1)^2+(-2R\sin\varphi)^2}d\varphi=2R\int\limits_{\varphi_1}^{\varphi_2}\sqrt{2+2\cos\varphi}d\varphi= }[/math]

[math]\displaystyle{ =2\sqrt{2}R\int\limits_{\varphi_1}^{\varphi_2}\sqrt{1+\cos\varphi}d\varphi=2\sqrt{2}R\int\limits_{\varphi_1}^{\varphi_2}\sqrt{2\cos^2\frac{\varphi}{2}}d\varphi=4R\int\limits_{\varphi_1}^{\varphi_2}\cos\frac{\varphi}{2}d\varphi= }[/math]

[math]\displaystyle{ =8R\int\limits_{\varphi_1}^{\varphi_2}\cos\frac{\varphi}{2}d\frac{\varphi}{2}=\left.8R\sin\frac{\varphi}{2}\right|_{\varphi_1}^{\varphi_2}=8R\left(\sin\frac{\varphi_2}{2}-\sin\frac{\varphi_1}{2}\right) \Rightarrow }[/math]

[math]\displaystyle{ \Rightarrow L_\text{дуг.кард}=8R\left(\sin\frac{\varphi_2}{2}-\sin\frac{\varphi_1}{2}\right) }[/math]

• Для вывода используется формула «длина дуги плоской кривой» в полярных координатах.

См. также

• Площадь сектора кардиоиды

Другие формулы

• длина дуги плоской кривой;
• длина дуги окружности;
• длина дуги параболы;
• длина дуги эллипса;
• длина дуги гиперболы;
• длина дуги синусоиды;
• длина дуги косинусоиды;
• длина дуги циклоиды;
• длина дуги кардиоиды;
• длина дуги астроиды;
• длина дуги эпициклоиды;
• длина дуги гипоциклоиды;
• длина дуги эвольвенты окружности;
• длина дуги цепной линии;
• длина дуги трактрисы;
• длина дуги лемнискаты Бернулли.

Литература

• Выгодский М. Я. Справочник по высшей математике — М.: Наука, 1964, стр.495.