Длина дуги плоской кривой — это числовая характеристика протяжённости дуги кривой на плоскости в единицах измерения длины.
Прямоугольная система координат[править]
Длина дуги плоской кривой, заданной уравнением y = y(x) или x = x(y), считается по формуле:
![{\displaystyle L_{\text{дуги}}=\int \limits _{x_{1}}^{x_{2}}{\sqrt {1+\left[y'_{x}(x)\right]^{2}}}dx\Leftrightarrow L_{\text{дуги}}=\int \limits _{x_{1}}^{x_{2}}{\sqrt {1+\left[{\frac {dy(x)}{dx}}\right]^{2}}}dx\Leftrightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6700e236f46513a7af3d090742d842783750687e)
![{\displaystyle \Leftrightarrow L_{\text{дуги}}=\int \limits _{y_{1}}^{y_{2}}{\sqrt {1+\left[x'_{y}(y)\right]^{2}}}dy\Leftrightarrow L_{\text{дуги}}=\int \limits _{y_{1}}^{y_{2}}{\sqrt {1+\left[{\frac {dx(y)}{dy}}\right]^{2}}}dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d87a369ba96f1c34447b6b7ed5a4153556dd34a)
Полярная система координат[править]
Длина дуги плоской кривой, заданной уравнением r = r(φ), считается по формуле:
![{\displaystyle L_{\text{дуги}}=\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {r^{2}(\varphi )+\left[r'_{\varphi }(\varphi )\right]^{2}}}d\varphi \Leftrightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4db9f67733c2d58f91927dae821f3092baa3d0cf)
![{\displaystyle \Leftrightarrow L_{\text{дуги}}=\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {r^{2}(\varphi )+\left[{\frac {dr(\varphi )}{d\varphi }}\right]^{2}}}d\varphi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/35b1faf7514f06897e1823a0ec2865e410f84646)
Параметрически заданная кривая[править]
Длина дуги плоской кривой, заданной (параметрически) уравнениями x = x(t), y = y(t), считается по формуле:
![{\displaystyle L_{\text{дуги}}=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left[x'_{t}(t)\right]^{2}+\left[y'_{t}(t)\right]^{2}}}dt\Leftrightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/106a80afa81679e15fc2b9084b03a996c6d6b367)
![{\displaystyle \Leftrightarrow L_{\text{дуги}}=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left[{\frac {dx(t)}{dt}}\right]^{2}+\left[{\frac {dy(t)}{dt}}\right]^{2}}}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3c566aebeb5c7556a06dca55e0acbd159c8249d)
Примеры плоских кривых[править]
Другие формулы[править]
- Бронштейн И. Н., Семендяев К. А. Справочник по математике — М., 1956, стр.394.
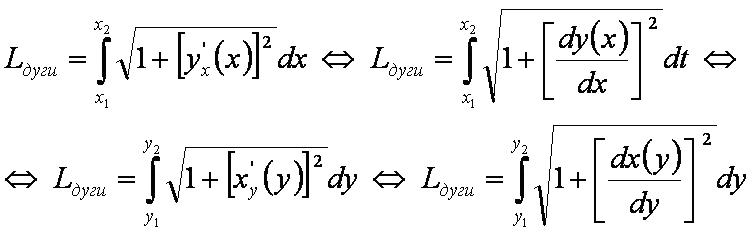
![{\displaystyle L_{\text{дуги}}=\int \limits _{x_{1}}^{x_{2}}{\sqrt {1+\left[y'_{x}(x)\right]^{2}}}dx\Leftrightarrow L_{\text{дуги}}=\int \limits _{x_{1}}^{x_{2}}{\sqrt {1+\left[{\frac {dy(x)}{dx}}\right]^{2}}}dx\Leftrightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6700e236f46513a7af3d090742d842783750687e)
![{\displaystyle \Leftrightarrow L_{\text{дуги}}=\int \limits _{y_{1}}^{y_{2}}{\sqrt {1+\left[x'_{y}(y)\right]^{2}}}dy\Leftrightarrow L_{\text{дуги}}=\int \limits _{y_{1}}^{y_{2}}{\sqrt {1+\left[{\frac {dx(y)}{dy}}\right]^{2}}}dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d87a369ba96f1c34447b6b7ed5a4153556dd34a)
![{\displaystyle L_{\text{дуги}}=\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {r^{2}(\varphi )+\left[r'_{\varphi }(\varphi )\right]^{2}}}d\varphi \Leftrightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4db9f67733c2d58f91927dae821f3092baa3d0cf)
![{\displaystyle \Leftrightarrow L_{\text{дуги}}=\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {r^{2}(\varphi )+\left[{\frac {dr(\varphi )}{d\varphi }}\right]^{2}}}d\varphi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/35b1faf7514f06897e1823a0ec2865e410f84646)
![{\displaystyle L_{\text{дуги}}=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left[x'_{t}(t)\right]^{2}+\left[y'_{t}(t)\right]^{2}}}dt\Leftrightarrow }](https://wikimedia.org/api/rest_v1/media/math/render/svg/106a80afa81679e15fc2b9084b03a996c6d6b367)
![{\displaystyle \Leftrightarrow L_{\text{дуги}}=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left[{\frac {dx(t)}{dt}}\right]^{2}+\left[{\frac {dy(t)}{dt}}\right]^{2}}}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3c566aebeb5c7556a06dca55e0acbd159c8249d)