Длина дуги эвольвенты окружности

Эвольвента окружности

Длина дуги эвольвенты окружности — это число, характеризующее протяжённость дуги эвольвенты окружности в единицах измерения длины.

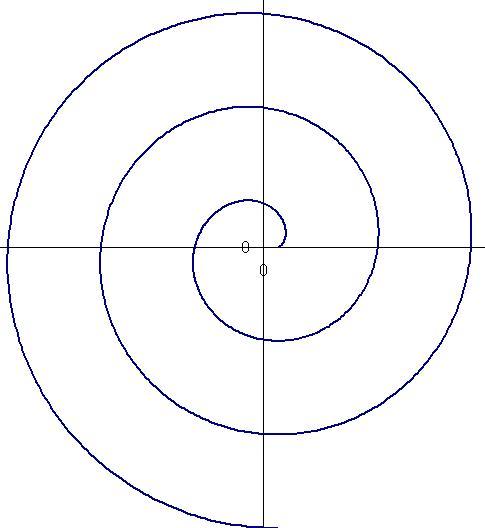
Эвольвента окружности — это линия, исходящая из начальной точки M₀ на окружности, описываемая точкой M (против часовой стрелки), лежащей (справа) на касательной к окружности в точке L и отстоящей от этой точки L на длину дуги окружности M₀L от начальной точки до этой точки.

Рассмотрим дуги эвольвенты окружности, исходящей из точки (R, 0).

Обозначения

Введём обозначения:

x₁ — абсцисса (меньшая) первой точки дуги;

y₁ — ордината первой точки дуги;

t₁ — параметр первой точки дуги;

x₂ — абсцисса (большая) второй точки дуги;

y₂ — ордината второй точки дуги;

t₂ — параметр второй точки дуги;

R — радиус окружности;

M = (x, y) — точка эвольвенты;

L — точка окружности;

M₀ = (R, 0) — начальная точка эвольвенты;

t — параметрическая переменная;

x = R(cost + tsint) — параметрическое уравнение абсциссы эвольвенты окружности;

y = R(sint − tcost) — параметрическое уравнение ординаты эвольвенты окружности;

L_{дуг.эвол} — длина дуги эвольвенты окружности.

Формула

$L_{\text{дуг.эвол}}={\frac {1}{2}}R\left(t_{2}^{2}-t_{1}^{2}\right),\ 0\leq t_{1}\leq t_{2}<\infty$

• Заметим, что длина дуги эвольвенты окружности M₀M от начальной точки равна L_t = Rt²/2.

Вывод формулы

$L_{\text{дуг.эвол}}=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left(x'_{t}(t)\right)^{2}+\left(y'_{t}(t)\right)^{2}}}dt=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left[\left(R\cos t+Rt\sin t\right)'_{t}\right]^{2}+\left[\left(R\sin t-Rt\cos t\right)'_{t}\right]^{2}}}dt=$

$=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left(Rt\cos t\right)^{2}+\left(Rt\sin t\right)^{2}}}dt=R\int \limits _{t_{1}}^{t_{2}}{\sqrt {t^{2}\cos ^{2}t+t^{2}\sin ^{2}t}}dt=$

$=R\int \limits _{t_{1}}^{t_{2}}tdt=\left.{\frac {1}{2}}Rt^{2}\right|_{t_{1}}^{t_{2}}={\frac {1}{2}}R\left(t_{2}^{2}-t_{1}^{2}\right)\Rightarrow L_{\text{дуг.эвол}}={\frac {1}{2}}R\left(t_{2}^{2}-t_{1}^{2}\right)$

• Для вывода используется формула длина дуги плоской кривой для функции, заданной параметрически, причём 0 < t₁ < t₂.

Другие формулы

• плоская кривая;
• окружность;
• парабола;
• эллипс;
• гипербола;
• синусоида;
• косинусоида;
• циклоида;
• кардиоида;
• астроида;
• эпициклоида;
• гипоциклоида;
• эвольвента;
• цепная линия;
• трактриса;
• лемниската Бернулли.

Литература

• Выгодский М. Я. Справочник по высшей математике — М.: Наука, 1964, стр.783.