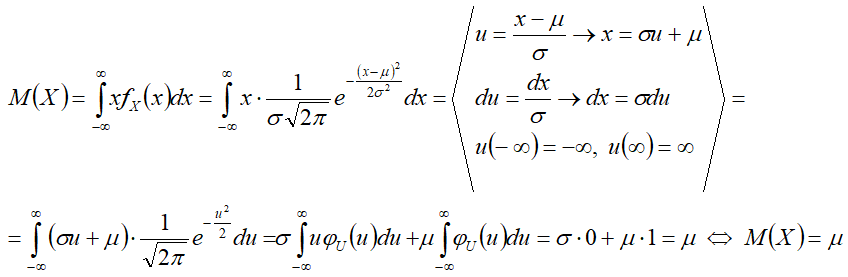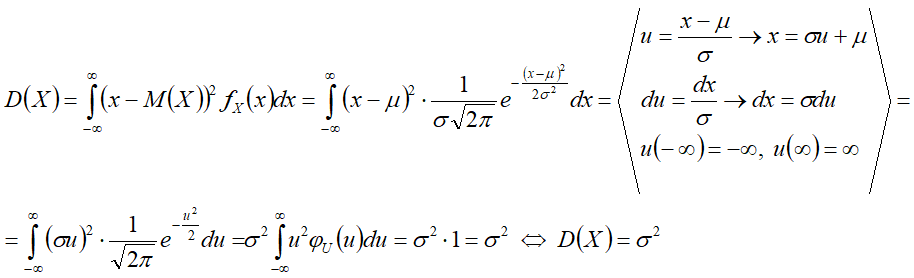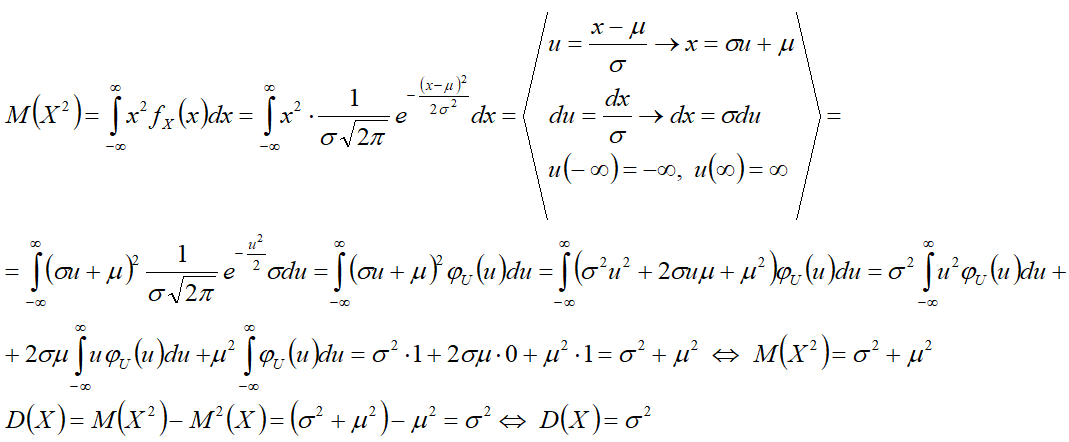Нормальное распределение

Нормальное Распределение за 6 Минут [6:24]

Мини-лекция А.М. Райгородского про нормальное распределение. Высшая математика // Математик МГУ (3 окт. 2021 г.) [26:05]

Нормальное распределение (распределение Гаусса) — двухпараметрическое распределение непрерывной случайной величины с экспонентой $e^{-{\frac {(x-{\text{μ}})^{2}}{2{\text{σ}}^{2}}}}$ в функциях распределения.

Обозначения

$X$ — случайная величина;

$U$ — стандартизованная случайная величина;

${\text{φ}}_{U}(u)$ — дифференциальная функция распределения стандартизованной случайной величины;

${\text{Φ}}_{U}(u)$ — интегральная функция распределения стандартизованной случайной величины;

$f_{X}(x)$ — дифференциальная функция распределения — функция плотности вероятности;

$F_{X}(x)$ — интегральная функция распределения — функция вероятности $P(X<x)$;

$M(X)={\text{μ}}$ — средняя — математическое ожидание;

$D(X)$ — дисперсия;

${\text{σ}}(X)={\text{σ}}$ — среднеквадратическое отклонение;

$Me(X)$ — медиана;

$Mo(X)$ — мода;

$As(X)$ — коэффициент асимметрии;

$Ek(X)$ — коэффициент эксцесса.

Функции распределения

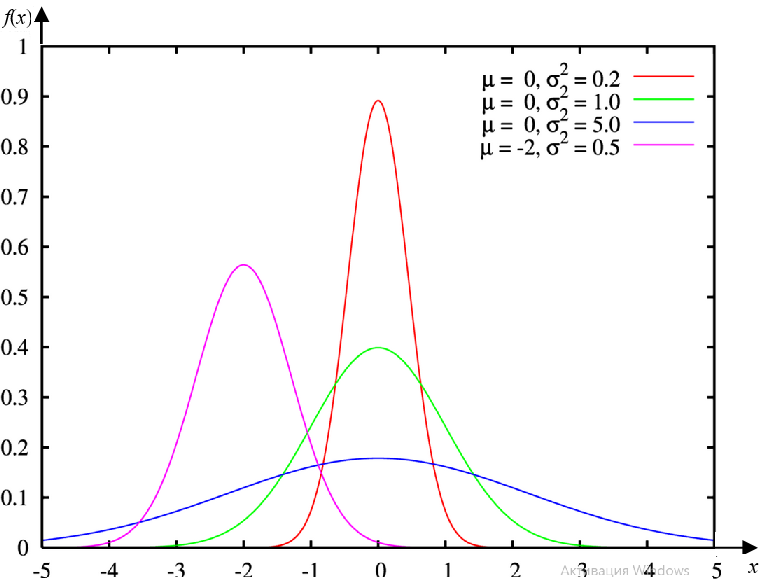
Дифференциальная функция

Формулы

$f_{X}(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\Leftrightarrow f_{X}(x)={\frac {1}{\sigma }}\varphi _{U}\left({\frac {x-\mu }{\sigma }}\right)$

Графики

• При ${\text{μ}}=0$ и ${\text{σ}}=1$ нормальное распределение называется Стандартное нормальное распределение.

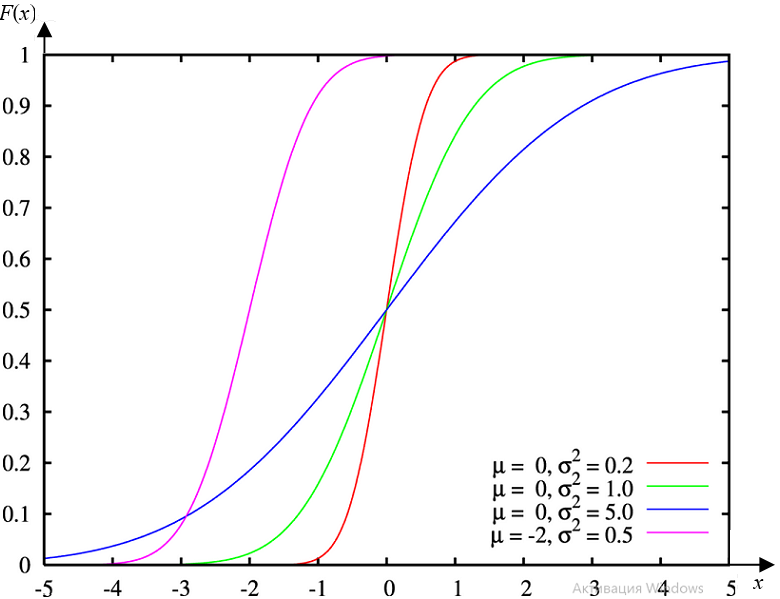
Интегральная функция

Формулы

$F_{X}(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\int \limits _{-\infty }^{x}e^{-{\frac {(t-\mu )^{2}}{2\sigma ^{2}}}}dt\Leftrightarrow F_{X}(x)={\frac {1}{\sigma }}\Phi _{U}\left({\frac {x-\mu }{\sigma }}\right)$

Графики

Характеристики

$M(X)=\mu$

$D(X)=\sigma ^{2}$

$\sigma (X)=\sigma$

$Me(X)=\mu$

$Mo(X)=\mu$

$As(X)=0$

$Ek(X)=0$

Вывод формул

Математическое ожидание

Дисперсия

1-й способ

2-й способ

Другие распределения

1. Распределения дискретной случайной величины:
   1. распределение Бернулли;
   2. биномиальное распределение;
   3. геометрическое распределение;
   4. гипергеометрическое распределение;
   5. дискретное равномерное распределение;
   6. логарифмическое распределение;
   7. распределение Пуассона;
2. Распределения непрерывной случайной величины:
   1. Бета-распределение;
   2. распределение Вейбулла;
   3. Гамма-распределение;
   4. распределение Гаусса;
   5. квадратичное распределение;
   6. распределение Коши;
   7. распределение Лапласа;
   8. линейное распределение;
   9. логистическое распределение;
   10. логнормальное распределение;
   11. нормальное распределение;
   12. распределение Парето;
   13. показательное распределение;
   14. непрерывное равномерное распределение;
   15. распределение Рэлея;
   16. распределение Сосновского;
   17. распределение Стьюдента;
   18. Ти-распределение;
   19. распределение Фишера-Снедекора;
   20. распределение Хи-квадрат;
   21. экспоненциальное распределение;
   22. Эл-распределение;
   23. Эф-распределение.

См. также

• Циклопедия:Списки:Объекты, названные в честь Гаусса

Литература

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.514.

Ссылки

• https://ru.wikipedia.org/wiki/Нормальное_распределение
• Участник:Logic-samara