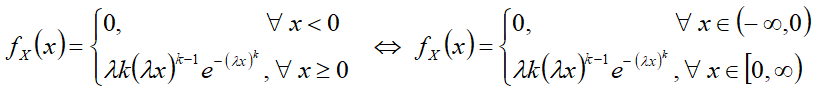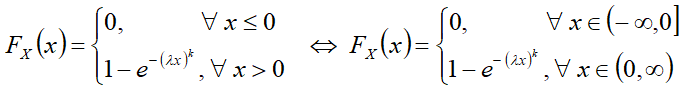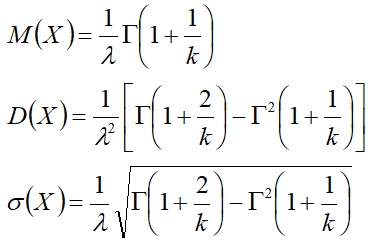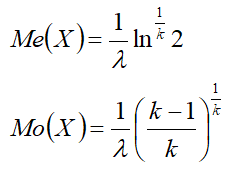Распределение Вейбулла
Перейти к навигации
Перейти к поиску
Распределение Вейбулла (двухпараметрическое) — это распределение непрерывной случайной величины с использованием экспоненты в функциях распределения.
Случайная величина наработки до отказа распределена по закону Вейбулла, в котором интенсивность отказов пропорциональна времени.
При этом:
при интенсивность отказов уменьшается со временем;
при интенсивность отказов не меняется со временем;
при интенсивность отказов увеличивается со временем.
Обозначения[править]
- — случайная величина;
- — параметр интенсивности, ;
- — параметр изменения интенсивности, ;
- — гамма-функция;
- — дифференциальная функция распределения — функция плотности вероятности;
- — интегральная функция распределения — функция вероятности ;
- — средняя — математическое ожидание;
- — дисперсия;
- — среднеквадратическое отклонение;
- — медиана;
- — мода;
- — коэффициент асимметрии;
- — коэффициент эксцесса.
Функции распределения:[править]
Дифференциальная функция[править]
Формулы[править]
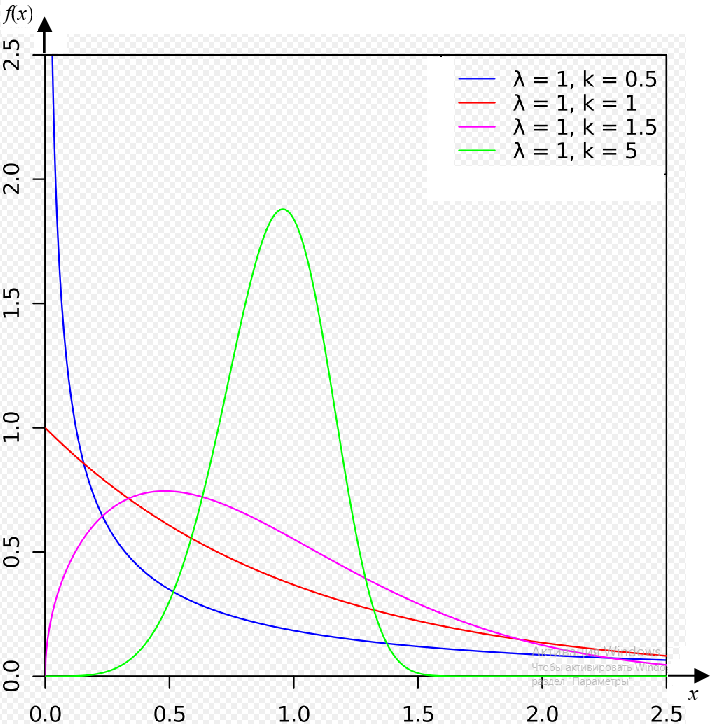
Графики[править]
- При распределение Вейбулла становится экспоненциальным.
- При распределение Вейбулла становится распределением Рэлея.
Интегральная функция[править]
Формулы[править]
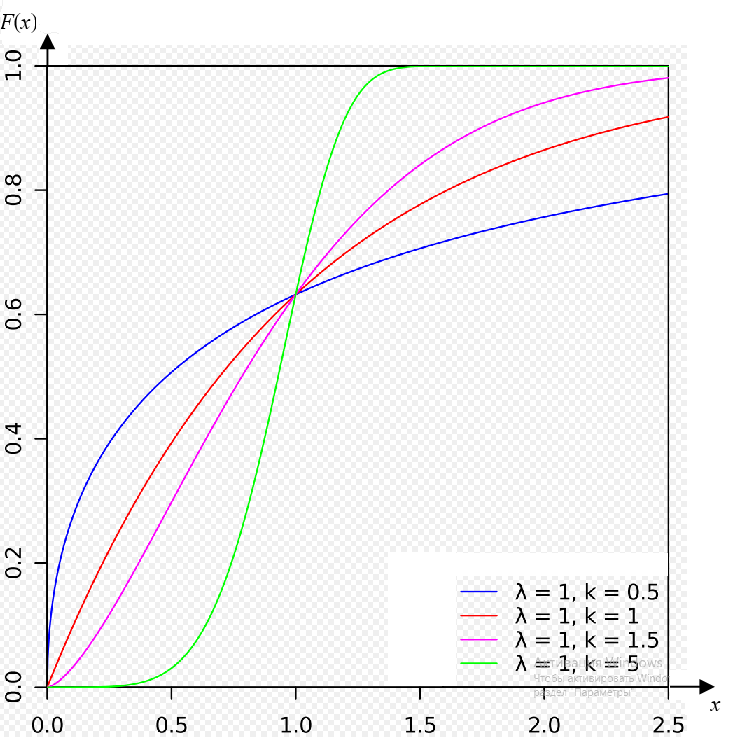
Графики[править]
Характеристики:[править]
Другие распределения:[править]
- Распределения дискретной случайной величины:
- Распределения непрерывной случайной величины:
- Бета-распределение;
- распределение Вейбулла;
- Гамма-распределение;
- распределение Гаусса;
- квадратичное распределение;
- распределение Коши;
- распределение Лапласа;
- линейное распределение;
- логистическое распределение;
- логнормальное распределение;
- нормальное распределение;
- распределение Парето;
- показательное распределение;
- непрерывное равномерное распределение;
- распределение Рэлея;
- распределение Сосновского;
- распределение Стьюдента;
- Ти-распределение;
- распределение Фишера-Снедекора;
- распределение Хи-квадрат;
- экспоненциальное распределение;
- Эл-распределение;
- Эф-распределение.
Ссылки[править]
| Файл:Bvn-small.png | Вероятностные распределения | |
|---|---|---|
| Одномерные | Многомерные | |
| Дискретные: | Бернулли | Биномиальное | Геометрическое | Гипергеометрическое | Логарифмическое | Отрицательное биномиальное | Пуассона | Дискретное равномерное | Мультиномиальное |
| Абсолютно непрерывные: | Бета | Вейбулла | Гамма- | Гиперэкспоненциальное | Гомпертца | Колмогорова | Коши | Лапласа | Логнормальное | Нормальное (Гаусса) | Логистическое | Накагами | Парето | Пирсона | Полукруговое | Непрерывное равномерное | Райса | Рэлея | Стьюдента | Трейси — Видома | Фишера | Хи-квадрат | Экспоненциальное | Variance-gamma | Многомерное нормальное | Копула |