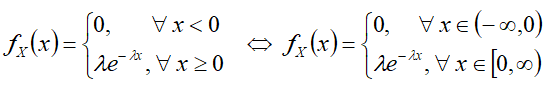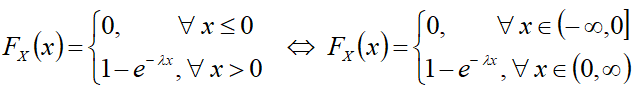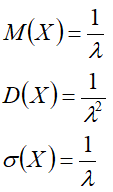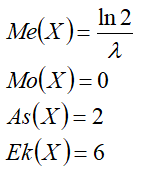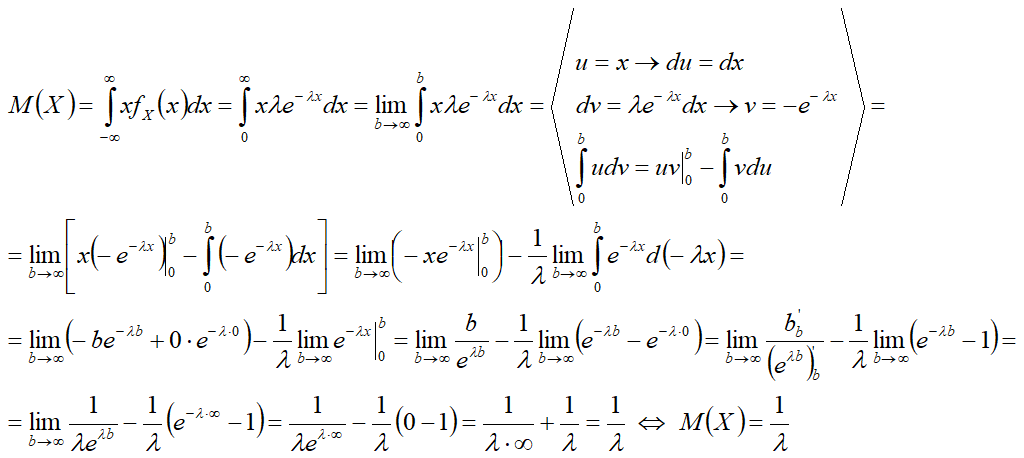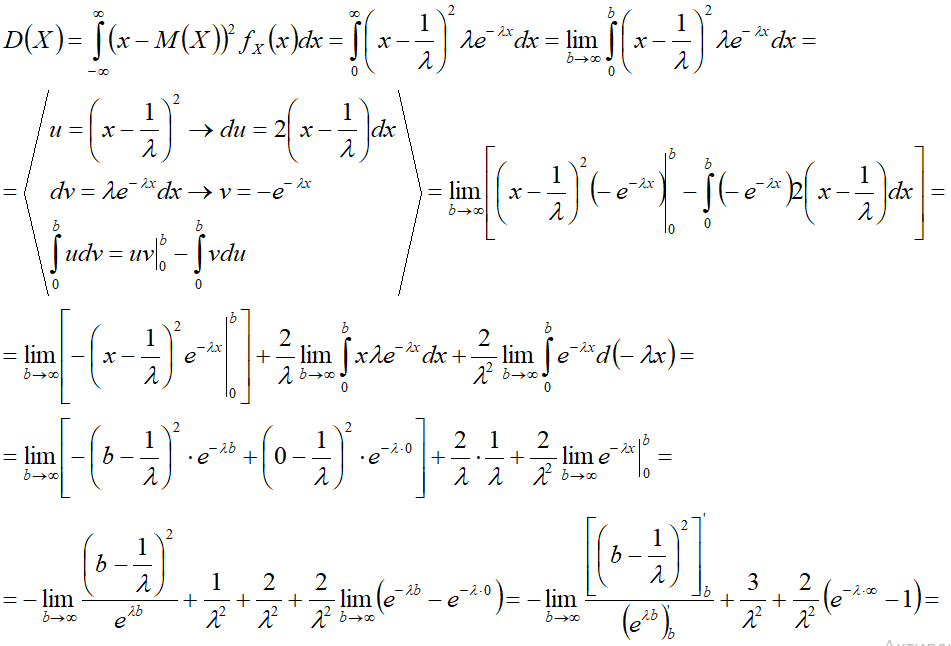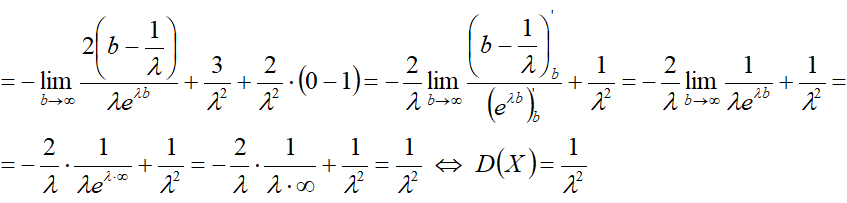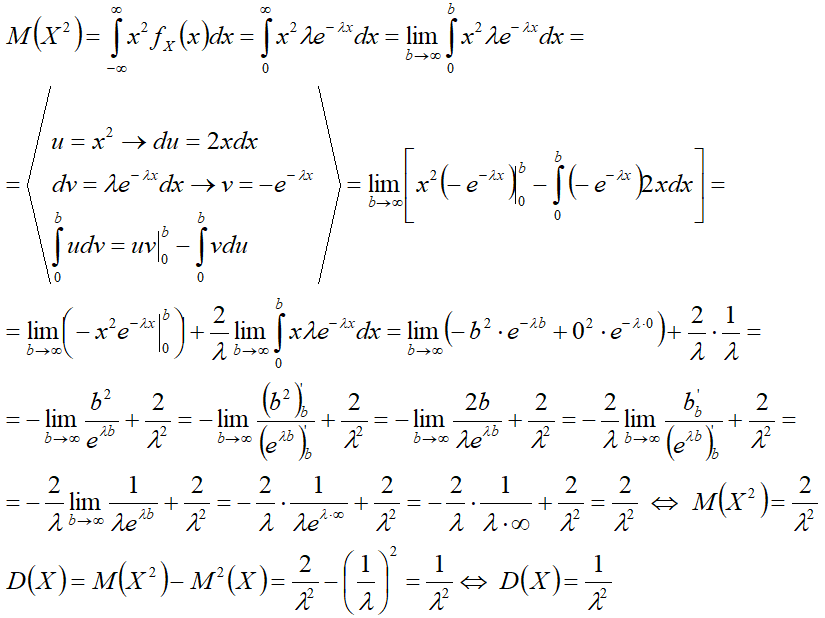Экспоненциальное распределение

Экспоненциальный закон распределения [8:25]

Экспоненциальное распределение (показательное распределение) — распределение непрерывной случайной величины, равной интервалу времени между двумя любыми соседними событиями в простейшем потоке с интенсивностью λ.

В функциях экспоненциального распределения есть экспонента e^-λx.

Обозначения

X — случайная величина;

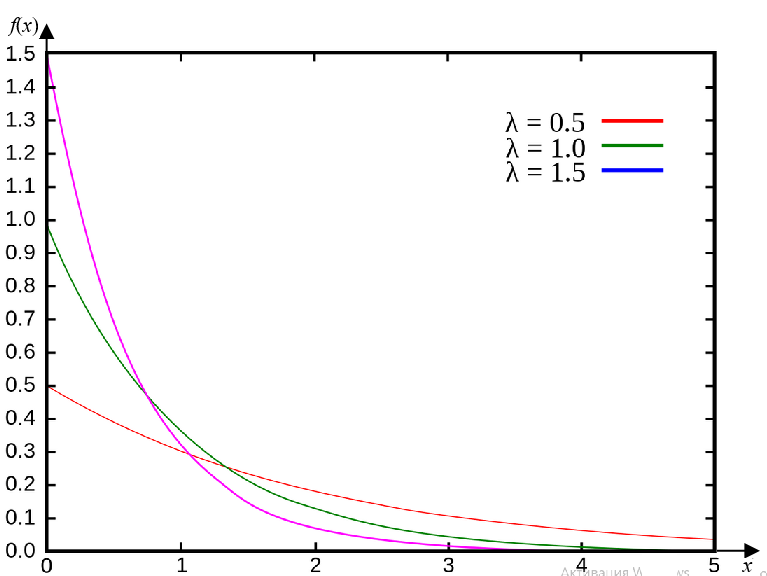
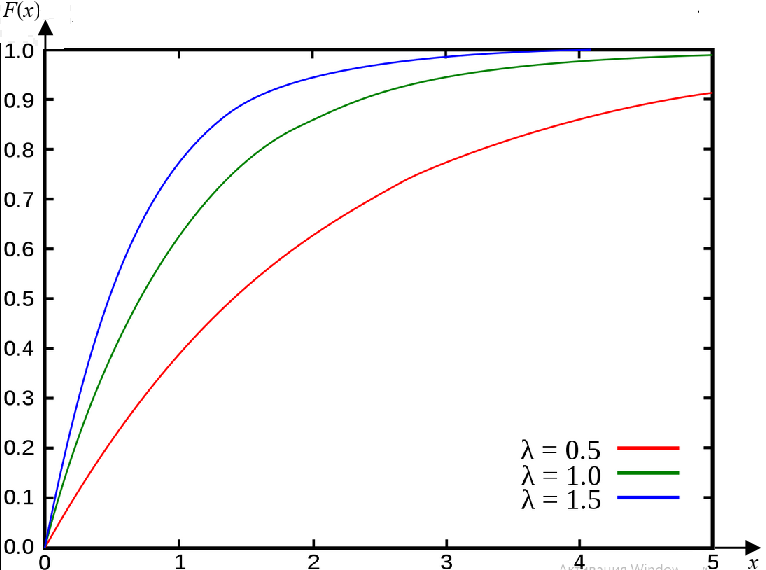
λ — интенсивность простейшего потока λ>0;

f_X(x) — дифференциальная функция распределения — функция плотности вероятности;

F_X(x) — интегральная функция распределения — функция вероятности P(X<x);

M(X) — средняя — математическое ожидание;

D(X) — дисперсия;

σ(X) — среднеквадратическое отклонение;

Me(X) — медиана;

Mo(X) — мода;

As(X) — коэффициент асимметрии;

Ek(X) — коэффициент эксцесса.

Функции распределения

Дифференциальная функция

Формулы

Графики

Интегральная функция

Формулы

Графики

Характеристики

Вывод формул

Математическое ожидание

Дисперсия

1-й способ

2-й способ

Другие распределения

1. Распределения дискретной случайной величины:
   1. распределение Бернулли;
   2. биномиальное распределение;
   3. геометрическое распределение;
   4. гипергеометрическое распределение;
   5. дискретное равномерное распределение;
   6. логарифмическое распределение;
   7. распределение Пуассона;
2. Распределения непрерывной случайной величины:
   1. Бета-распределение;
   2. распределение Вейбулла;
   3. Гамма-распределение;
   4. распределение Гаусса;
   5. квадратичное распределение;
   6. распределение Коши;
   7. распределение Лапласа;
   8. линейное распределение;
   9. логистическое распределение;
   10. логнормальное распределение;
   11. нормальное распределение;
   12. распределение Парето;
   13. показательное распределение;
   14. непрерывное равномерное распределение;
   15. распределение Рэлея;
   16. распределение Сосновского;
   17. распределение Стьюдента;
   18. Ти-распределение;
   19. распределение Фишера-Снедекора;
   20. распределение Хи-квадрат;
   21. экспоненциальное распределение;
   22. Эл-распределение;
   23. Эф-распределение.

Литература

• Овчаров Л. А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969, стр.18.

Ссылки

• Участник:Logic-samara