Объём тора

Тор

Объём тора — число, характеризующее объём, ограниченный тором, в единицах измерения объёма.

Тор — поверхность вращения образующей окружности вокруг оси, лежащей в плоскости этой окружности и не проходящей через её центр.

Обозначения

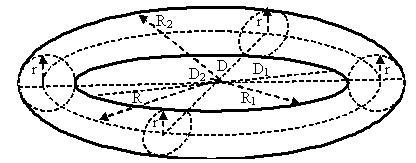
R — радиус окружности вращения образующей окружности тора;

r — радиус образующей окружности тора;

R₂ — внешний радиус тора;

R₁ — внутренний радиус тора;

D — диаметр окружности вращения образующей окружности тора;

d — диаметр образующей окружности тора;

D₂ — внешний диаметр тора;

D₁ — внутренний диаметр тора;

S_тор — площадь тора;

V_тор — объём тора.

Формулы

$V_{\text{тор}}=2\pi ^{2}Rr^{2}\Leftrightarrow V_{\text{тор}}={\frac {1}{2}}rS_{\text{тор}},\ S_{\text{тор}}=4\pi ^{2}Rr\Leftrightarrow$

$\Leftrightarrow V_{\text{тор}}={\frac {1}{4}}\pi ^{2}Dd^{2},\ D=2R,\ d=2r\Leftrightarrow$

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \Leftrightarrow V_{\text{тор}}=\pi ^{2}(R_{1}+R_{2})r^{2},\ R={\frac {R_{1}+R_{2}}{2}}\Leftrightarrow }

$\Leftrightarrow V_{\text{тор}}={\frac {1}{8}}\pi ^{2}(D_{1}+D_{2})d^{2},\ D={\frac {D_{1}+D_{2}}{2}}$

Вывод формулы

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle V_{\text{тор}}=\pi \int \limits _{-r}^{r}\left[\left(R+{\sqrt {r^{2}-x^{2}}}\right)^{2}-\left(R-{\sqrt {r^{2}-x^{2}}}\right)^{2}\right]dx=\pi \int \limits _{-r}^{r}4R{\sqrt {r^{2}-x^{2}}}dx=}

$=8\pi R\int \limits _{0}^{r}{\sqrt {r^{2}-x^{2}}}dx=\left.4\pi R\left(x{\sqrt {r^{2}-x^{2}}}+r^{2}\arcsin {\frac {x}{r}}\right)\right|_{0}^{r}=4\pi Rr^{2}\arcsin 1=$

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle =4\pi Rr^{2}{\frac {\pi }{2}}=2\pi ^{2}Rr^{2}\Rightarrow V_{\text{тор}}=2\pi ^{2}Rr^{2}}

Использовано, что:

$\int {\sqrt {a^{2}-x^{2}}}\;dx={\frac {1}{2}}\left(x{\sqrt {a^{2}-x^{2}}}+a^{2}\arcsin {\frac {x}{a}}\right)+C$

См. также

• Площадь тора

Другие формулы

1. фигура вращения;
2. шар;
3. цилиндр;
4. конус;
5. усечённый цилиндр;
6. усечённый конус;
7. шаровой сегмент;
8. шаровой сектор;
9. шаровой слой;
10. шаровой клин;
11. центральный шаровой клин;
12. торовый клин;
13. цилиндрическая труба;
14. цилиндрическое копыто;
15. конусное копыто;
16. шаровое копыто;
17. параболоидное копыто;
18. шаровая бочка;
19. круговая бочка;
20. параболическая бочка;
21. сегментное кольцо;
22. тор;
23. кокон;
24. купол;
25. сфероид;
26. параболоид вращения.

Литература

• Бронштейн И. Н., Семендяев К. А., Справочник по математике — М., 1956, стр.178.