Объём шарового сегмента

Шаровой сегмент

30. Объем шара, шарового сегмента, слоя и сектора // Инфоурок [8:57]

Формулы

Объём шарового сегмента — часть объёма шара, ограниченная сегментом сферы и основанием сегмента. Вычисляется по формуле:

V = πh²(3R − h)/3

(R — радиус шара, h — высота шарового сегмента, π — число Пи).

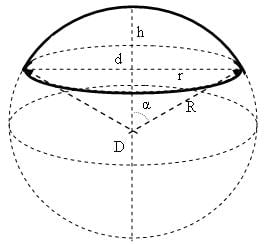
Обозначения[править]

R — радиус шара;

r — радиус основания шарового сегмента;

h — высота шарового сегмента;

V_сегм — объём шарового сегмента.

V_{\text{сегм}}=\pi Rh^{2}-{\frac {1}{3}}\pi h^{3}\Leftrightarrow

\Leftrightarrow V_{\text{сегм}}={\frac {1}{3}}\pi h^{2}(3R-h),\ R={\frac {h^{2}+r^{2}}{2h}}\Leftrightarrow

\Leftrightarrow V_{\text{сегм}}={\frac {1}{6}}\pi h(h^{2}+3r^{2}),\ r={\sqrt {2Rh-h^{2}}}\Leftrightarrow

\Leftrightarrow V_{\text{сегм}}={\frac {1}{3}}\pi h(3Rh-h^{2}),\ h={\sqrt {2Rh-r^{2}}}\Leftrightarrow

\Leftrightarrow V_{\text{сегм}}={\frac {1}{3}}\pi h(Rh+r^{2}),\ h=R-sign(R-h)\cdot {\sqrt {R^{2}-r^{2}}}\Leftrightarrow

\Leftrightarrow V_{\text{сегм}}={\frac {1}{3}}\pi R^{3}(2-3\cos \alpha +\cos ^{3}\alpha ),\ h=R(1-\cos \alpha ),r=R\sin \alpha

Заметим, что при высоте сегмента равной диаметру шара, сегмент превращается в шар. Соответственно, формула объёма сегмента с высотой в диаметр шара превращается в формулу объёма шара.

V_{\text{сегм}}=\pi \int \limits _{R-h}^{R}\left({\sqrt {R^{2}-x^{2}}}\right)^{2}dx=\pi \int \limits _{R-h}^{R}(R^{2}-x^{2})dx=\pi \left.\left(R^{2}x-{\frac {x^{3}}{3}}\right)\right|_{R-h}^{R}=

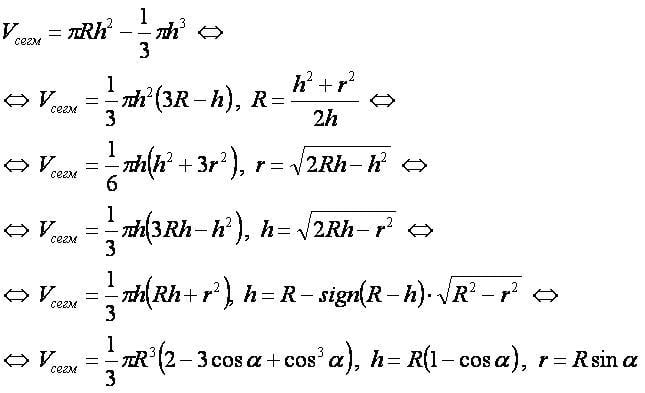
=\pi \left[R^{2}h-{\frac {1}{3}}R^{3}+{\frac {1}{3}}(R-h)^{3}\right]=\pi \left(Rh^{2}-{\frac {1}{3}}h^{3}\right)={\frac {1}{3}}\pi h^{2}(3R-h)\Rightarrow

\Rightarrow V_{\text{сегм}}={\frac {1}{3}}\pi h^{2}(3R-h)