Площадь поверхности усечённого цилиндра

Усечённый цилиндр

Развертка усеченного цилиндра [2:18]

Площадь поверхности усечённого цилиндра — это сумма площадей основания, сечения и боковой поверхности усечённого цилиндра.

Рассмотрим прямые круговые усечённые цилиндры без сечения основания.

Обозначения

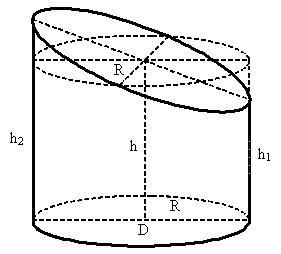
$R$ — радиус основания цилиндра;

$D$ — диаметр основания цилиндра;

$h$ — средняя высота усечённого цилиндра;

$h_{1}$ — наименьшая высота усечённого цилиндра;

$h_{2}$ — наибольшая высота усечённого цилиндра;

$S_{\text{осн}}$ — площадь основания усечённого цилиндра;

$S_{\text{сеч}}$ — площадь сечения усечённого цилиндра;

$S_{\text{бок}}$ — площадь боковой поверхности усечённого цилиндра;

$S_{\text{усеч.цил}}$ — площадь поверхности усечённого цилиндра.

Формула

$S_{\text{усеч.цил}}=\pi R\left[R+h_{1}+h_{2}+{\sqrt {R^{2}+{\frac {1}{4}}(h_{2}-h_{1})^{2}}}\right],\ h={\frac {h_{1}+h_{2}}{2}}\Leftrightarrow$

$\Leftrightarrow S_{\text{усеч.цил}}={\frac {1}{4}}\pi D\left[D+2h_{1}+2h_{2}+{\sqrt {D^{2}+(h_{2}-h_{1})^{2}}}\right],\ D=2R\Leftrightarrow$

$\Leftrightarrow S_{\text{усеч.цил}}=S_{\text{бок}}+S_{\text{осн}}+S_{\text{сеч}},\ S_{\text{бок}}=2\pi Rh,\ S_{\text{осн}}=\pi R^{2},\ S_{\text{сеч}}=\pi R{\sqrt {R^{2}+{\frac {1}{4}}(h_{2}-h_{1})^{2}}}$

См. также

• Объём усечённого цилиндра

Другие формулы

1. фигура вращения;
2. шар;
3. цилиндр;
4. конус;
5. усечённый цилиндр;
6. усечённый конус;
7. шаровой сегмент;
8. шаровой сектор;
9. шаровой слой;
10. шаровой клин;
11. центральный шаровой клин;
12. торовый клин;
13. цилиндрическая труба;
14. цилиндрическое копыто;
15. конусное копыто;
16. шаровое копыто;
17. шаровая бочка;
18. круговая бочка;
19. сегментное кольцо;
20. тор;
21. кокон;
22. купол;
23. сфероид;
24. параболоид вращения.

Литература

• Бронштейн И. Н., Семендяев К. А. Справочник по математике — М., 1956, стр.175.