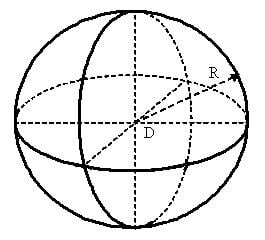
Площадь сферы

Шар

1710. В.П. Минорский. Площадь сферы [6:37]

Площадь сферы — число, характеризующее сферу (поверхность шара) в единицах измерения площади.

Обозначения

R — радиус шара;

D — диаметр шара;

S_сф — площадь сферы.

Формула

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle S_\text{сф}=4\pi R^2\Leftrightarrow S_\text{сф}=\frac{3}{R}V_\text{сф},\ V_\text{шар}=\frac{4}{3}\pi R^3\Leftrightarrow S_\text{сф}=\pi D^2,\ D=2R}

Вывод формулы

По формуле для фигуры вращения:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle S_\text{сф}=2\pi\int\limits_{-R}^R\sqrt{R^2-x^2}\sqrt{1+\left(\sqrt{R^2-x^2}^{\text{ }'}\right)^2}dx=2\pi\int\limits_{-R}^R\sqrt{R^2-x^2}\sqrt{1+\left(\frac{-x}{\sqrt{R^2-x^2}}\right)^2}dx=}

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle =2\pi\int\limits_{-R}^R Rdx = 4\pi R\int\limits_0^R 1dx=\left.4\pi Rx\right|_0^R=4\pi R^2\Rightarrow S_\text{сф}=4\pi R^2}

Другие формулы

1. фигура вращения;
2. шар;
3. цилиндр;
4. конус;
5. усечённый цилиндр;
6. усечённый конус;
7. шаровой сегмент;
8. шаровой сектор;
9. шаровой слой;
10. шаровой клин;
11. центральный шаровой клин;
12. торовый клин;
13. цилиндрическая труба;
14. цилиндрическое копыто;
15. конусное копыто;
16. шаровое копыто;
17. шаровая бочка;
18. круговая бочка;
19. сегментное кольцо;
20. тор;
21. кокон;
22. купол;
23. сфероид;
24. параболоид вращения.

Литература

• Бронштейн И. Н., Семендяев К. А., Справочник по математике — М., 1956, стр.177.