Площадь арки циклоиды
Перейти к навигации
Перейти к поиску
Площадь арки циклоиды — это число, характеризующее арку (или часть арки) циклоиды в единицах измерения площади.
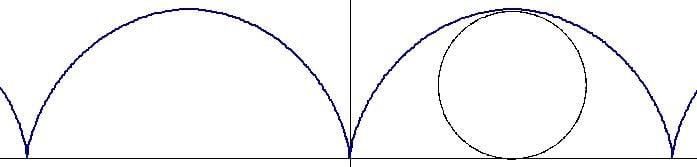
Арка циклоиды — это область, ограниченная циклоидой и осью абсцисс при 0 ≤ x ≤ 2π.
Рассмотрим арки циклоиды при 0 ≤ t ≤ 2π.
Обозначения[править]
Введём обозначения:
x1 — абсцисса первой точки дуги;
y1 — ордината первой точки дуги;
t1 — параметр (меньший) первой точки дуги;
x2 — абсцисса второй точки дуги;
y2 — ордината второй точки дуги;
t2 — параметр (больший) второй точки дуги;
R — радиус производящей окружности;
t — параметрическая переменная;
x = R(t − sint) — параметрическое уравнение абсциссы циклоиды;
y = R(1 − cost) — параметрическое уравнение ординаты циклоиды;
Sцикл — площадь арки (или части арки) циклоиды.
Формула[править]
- Площадь полной (от 0 до 2π) арки циклоиды равна площади трёх производящих кругов, Sарк.цикл = 3πR2.
Вывод формулы[править]
- Для вывода используется формула «площадь плоской фигуры» в параметрической форме.
См. также[править]
Другие формулы[править]
- плоская фигура;
- круг;
- сегмент круга;
- сектор круга;
- сегмент правильного многоугольника;
- сектор правильного многоугольника;
- серп;
- сегмент параболы;
- эллипс;
- сегмент эллипса;
- сектор эллипса;
- серп эллипса;
- сегмент гиперболы;
- арка синусоиды;
- арка косинусоиды;
- фигура, ограниченная тангенсоидой и осью абсцисс;
- фигура, ограниченная котангенсоидой и осью абсцисс;
- арка циклоиды;
- сектор кардиоиды;
- фигура, ограниченная цепной линией и осью абсцисс;
- фигура, ограниченная трактрисой и осью абсцисс;
- сектор лемнискаты Бернулли.
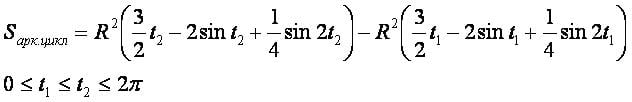


![{\displaystyle S_{\text{арк.цикл.}}=\int \limits _{t_{1}}^{t_{2}}R(1-\cos t)[R(t-\sin t)]_{t}^{'}dt=\int \limits _{t_{1}}^{t_{2}}R^{2}(1-\cos t)^{2}dt=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bed505cd726d79d82d3dff0b9cd1fc8def52c061)


