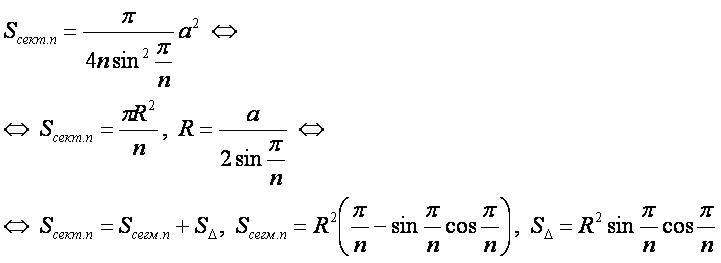Площадь сектора правильного n-угольника

Формулы

Площадь сектора правильного n-угольника — это число, характеризующее сектор правильного n-угольника в единицах измерения площади.

Сектор правильного n-угольника — это меньший сектор описанной окружности (построенный на стороне) правильного n-угольника.

Обозначения

Введём обозначения:

a — длина стороны;

n — число сторон;

R — радиус описанной окружности;

α — половинный центральный угол, α=π/n;

S_Δ — площадь равнобедренного треугольника с основанием равным стороне и боковыми сторонами равными радиусу описанной окружности;

S_сегм.n — площадь сегмента описанной окружности правильного n-угольника;

S_сект.n — площадь сектора описанной окружности правильного n-угольника.

Формулы

$S_{\text{сект.n}}={\frac {\pi }{4n\sin ^{2}{\frac {\pi }{n}}}}a^{2}\Leftrightarrow$

$\Leftrightarrow S_{\text{сект.n}}={\frac {\pi R^{2}}{n}},\ R={\frac {a}{2\sin {\frac {\pi }{n}}}}\Leftrightarrow$

$\Leftrightarrow S_{\text{сект.n}}=S_{\text{сегм.n}}+S_{\triangle },\ S_{\text{сегм.n}}=R^{2}\left({\frac {\pi }{n}}-\sin {\frac {\pi }{n}}\cos {\frac {\pi }{n}}\right),\ S_{\triangle }=R^{2}\sin {\frac {\pi }{n}}\cos {\frac {\pi }{n}}$

Другие формулы

• плоская фигура;
• круг;
• сегмент круга;
• сектор круга;
• сегмент правильного многоугольника;
• сектор правильного многоугольника;
• серп;
• сегмент параболы;
• эллипс;
• сегмент эллипса;
• сектор эллипса;
• серп эллипса;
• сегмент гиперболы;
• арка синусоиды;
• арка косинусоиды;
• фигура, ограниченная тангенсоидой и осью абсцисс;
• фигура, ограниченная котангенсоидой и осью абсцисс;
• арка циклоиды;
• сектор кардиоиды;
• фигура, ограниченная цепной линией и осью абсцисс;
• фигура, ограниченная трактрисой и осью абсцисс;
• сектор лемнискаты Бернулли.