Комплексные числа
Комплексные числа (complexus — «соплетённый», составной, сложный) — математическая концепция чисел-сумм вещественного и чисто мнимого числа — вещественного множителя абстрактной квази-величины мнимая единица i, которая инверсивно определяется через утверждение, что её квадрат равен минус единице.
Более формально: комплексное число — это число, которое записывается в алгебраической форме в виде , где a и b — любые вещественные чи́сла, и считается, что для числа́ выполняется тождество .
Множество комплексных чисел в традиционной нотации обозначается зна́ком .
История[править]
Комплексные числа появились в XVI веке, когда математики попытались решить квадратные уравнения с отрицательными дискриминантами (такие уравнения не имеют вещественных корней). Оказалось, что квадратный корень из отрицательного числа приходится извлекать при решении кубического уравнения по формуле, хотя все корни исходного кубического уравнения могут быть вещественными. Тогда же появилось описание действий над комплексными числами в их современном понимании (эти действия было необходимо проводить с комплексными числами для корректного решения кубического уравнения по формуле).
Значимый вклад в теорию комплексных чисел внес великий математик Леонард Эйлер (XVIII век), разработавший привычные алгебраическую, тригонометрическую и показательную записи комплексного числа. В XIX веке появилось отображение комплексных чисел на координатной плоскости, методы комплексного анализа.
Основная теорема алгебры утверждает, что всякий многочлен n-й степени с комплексными коэффициентами может быть разложен на n линейных сомножителей, и, таким образом, у всякого полиномиального уравнения n-й степени есть n корней в поле комплексных чисел с учетом их кратностей (до появления комплексных чисел у полиномиального уравнения могло не быть корней вовсе).
Свойства[править]
В алгебраической форме комплексное число записывается как , где под понимается , то есть выполняется тождество . Мнимая часть появляется при извлечении квадратного корня из отрицательного вещественного числа: .
Над комплексными числами можно проводить операции сложения (вычитания), умножения (по правилам перемножения многочленов), деления.
Формула деления комплексных чисел:
- ,
то есть для каждого ненулевого комплексного число можно найти обратное к нему по умножению.
Поэтому они образуют поле, которое расширяет поле вещественных чисел: . Вещественные числа в этой модели — комплексные, коэффициент при мнимой части которых равен 0.
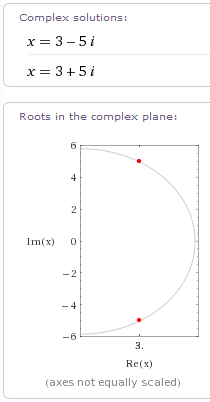
Пара сопряженных комплексных чисел является решением квадратного уравнения при . Например, в уравнении имеем ; в таком случае , где . Решения уравнения, соответственно .
Сумма и произведение сопряженных комплексных чисел представляют собой вещественные числа.
Комплексные числа изучаются в специальном разделе математического анализа — комплексном анализе, в алгебре они доставляют пример алгебраически замкнутого поля, имеют значительное применение в физике.
Геометрическая интерпретация[править]
Комплексное число z = a + bi может быть изображено точкой (a; b) на комплексной плоскости, на которой по оси x располагаются вещественные числа, по оси y — чисто мнимые.
Тригонометрическая форма отражает вектор, отложенный от начала координат до этой точки.
Тригонометрическая форма комплексного числа: , где |z| («модуль z») — расстояние на комплексной плоскости от начала координат до точки, обозначающей число z, а «аргумент» = (если ), (если ) и (если ).
При возведении комплексного числа в степень достаточно возвести только его модуль, а аргумент домножить на показатель степени:
Показательная форма комплексного числа, открытая Эйлером: , где r — модуль комплексного числа, а — его аргумент.
Операции с комплексными числами[править]
- сложение чисел;
- вычитание чисел;
- умножение чисел;
- деление чисел;
- обращение числа;
- возведение в степень;
- извлечение квадратного корня;
- извлечение кубического корня;
- извлечение корня n-ой степени;
- логарифмирование числа;
- возведение в комплексную степень;
- тригонометрические функции комплексных чисел;
- гиперболические функции комплексных чисел;
- взятие комплексно сопряжённого числа;
Литература[править]
- Абрамович М. И., Стародубцев М. Т. Математика (геометрия и тригонометрические функции). М., 1976.
Числовые системы ↑ | |
|---|---|
множества |
Натуральные числа () • Целые () • Рациональные () • Алгебраические () • Периоды • Вычислимые |
и их расширения |
Действительные (вещественные) () • Комплексные () • Кватернионы () • Числа Кэли (октавы, октонионы) () • Седенионы () • Альтернионы • Дуальные • Гиперкомплексные • Супердействительные • Гипервещественные |
числовые системы |
Кардинальные числа • Порядковые (трансфинитные, ординалы) • p-адические • Сверхнатуральные • Сюрреальные |
|
Двойные • Иррациональные • Трансцендентные • Числовой луч • Положительные числа • Простые числа • Бикватернионы • Координатизация • Расширение понятия числа | |