Формула Эйлера

06. Формула Эйлера // MATLABinRussia (Алексей Савватеев) [13:15]

Формула Эйлера — формула в теории комплексной переменной, которая связывает тригонометрию и комплексное возведение в степень:

$e^{ix}=\cos x+i\,\sin x.$

Она лежит в основе тождества Эйлера e^iπ + 1 = 0, которое сообществом часто признаётся как «самое красивое утверждение в математике» (почему-то).

Предварительно

Прежде всего: формула Эйлера — это не аксиома и не определение комплексной экспоненты. Это именно теорема. Прояснив этот момент, мы ниже подробно обрисуем причину, почему те или иные люди совершенно не понимают, как это вообще — возводить в мнимую степень. Разрешение же этого непонимания будет дано в определении этого возведения.

Старшекласснику или студенту, который только что прошёл извлечение комплексного числа корня целой степени n, наверное, известно, что такая операция является |n|-значной. Связано это с тем фактом, что при умножении комплексных чисел их аргументы складываются, а значит, при возведении в n-ю степень аргумент множится на n, а следовательно, в силу того, что поворот является операцией с периодом в τ радиан, действие, обратное этому возведению, должно порождать неоднозначность. Причём эта неоднозначность порождает на комплексной плоскости правильный |n|-угольник с центром в 0 + 0i.

И, рассуждая именно так, этот человек может задать определение такой операции, как возведение в степень аликвотной дроби 1/n, как извлечение корня n-й степени, которое по-прежнему будет возвращать вершины правильного многоугольника. Вроде бы стройно и красиво.

Однако, если ему захочется это обобщить на случай любых рациональных чисел, возникнет проблема: между двумя определениями, казалось бы похожими:

$x^{m/n}={\sqrt[{n}]{x^{m}}}\qquad {\text{vs}}\qquad x^{m/n}={\sqrt[{n}]{x}}^{m}$

есть жёсткая грань: первое из них абсолютно непонятно, сколько вообще должно возвращать значений, учитывая, что любую дробь m/n можно ведь представить как 2m/(2n), 3m/(3n), 100500m/(100500n) и так далее. А нам ведь хочется относиться к дроби m/n как к некоему неделимому, цельному объекту, как к числу, а не как к паре, так сказать, функционально не связанных друг с другом чисел. Поэтому дроби m/n, 2m/(2n), 3m/(3n) и тому подобные должны восприниматься как абсолютно равнозначные объекты и этот факт не должен вести себя как дышло, влияя на определение степени x^m/n. Поэтому оптимальнее как бы договориться брать не первое, а второе определение: при нём такой неопределённости не будет, так как в дроби вида km/(kn) число k в числителе совершенно всегда как бы «уничтожает» неоднозначность, которую вызывает число k в знаменателе, и при таком определении такое возведение в степень возвращает n/НОД(m, n) комплексных чисел.

Но что делать с иррациональной степенью? Ведь иррациональные числа из рациональных получаются исключительно как их пределы при стремлении числителя и знаменателя к ∞. И что? Получится бесконечнозначная функция, у которой проще будет просто извлечь модуль, потому что у них он одинаков, и работать лишь с ним? Чувствуете пессимистичную тенденцию?

В свете этого старшекласснику или студенту человеку непонятно: а что вообще значит возвести в чисто мнимую степень? Или вообще в комплексную? Что это за «сферическая операция в вакууме», которую математики и физики каким-то телепатическим образом уловили и с которой пытаются работать? Возможно, такой непонятливый человек в курсе такой вещи, как главное значение функции. Но всё равно вопросов становится не меньше: а как это «главное значение» выделить и обосновать для комплексного возведения?

Определение

Итак, для спасения от этой неурядицы используется определение числа Эйлера. И желательно не такое:

$e=\lim _{x\to 0}(1+x)^{1/x},$

где не гарантируется, что в ходе стремления число 1/x будет всегда сохраняться целым, а такое:

$e=\lim _{\underset {x\to \infty }{x\in \mathbb {Z} }}(1+{\frac {1}{x}})^{x}.$

Заметим, что для целой степени n верна теорема:

$e^{n}=\lim _{\underset {x\to \infty }{x\in \mathbb {Z} }}(1+{\frac {1}{x}})^{xn}=\lim _{\underset {x\to \infty }{x\in \mathbb {Z} }}(1+{\frac {n}{xn}})^{xn}=\lim _{\underset {x\to \infty }{x\in \mathbb {Z} }}(1+{\frac {n}{x}})^{x}.$

И именно это позволяет обобщить такое возведение на любую комплексную степень n:

$e^{n}\equiv \lim _{\underset {x\to \infty }{x\in \mathbb {Z} }}(1+{\frac {n}{x}})^{x}.$

Именно такое определение и называют главным значением натуральной экспоненты комплексного числа. Также равносильно это определение можно переписать в виде ряда Маклорена — Тейлора как

$e^{n}=\sum _{o=0}^{\infty }{\frac {n^{o}}{o!}}.$

Любопытно, что для такого определения сохраняются правила сложения и вычитания степеней, что мы знаем со школы. Также верно, что:

$\left(\lim _{x}(1+{\frac {n}{x}})^{x}\right)'_{n}=\lim _{x}(1+{\frac {n}{x}})^{x}.$

Доказательство

Самое наглядное

Доказательство через производную. Оси Re и Im расположены нетрадиционным образом — положительной ориентацией получается вращение по часовой стрелке.

Самое наглядное доказательство задействует два факта:

• |e^ix| = 1 при вещественном иксе;
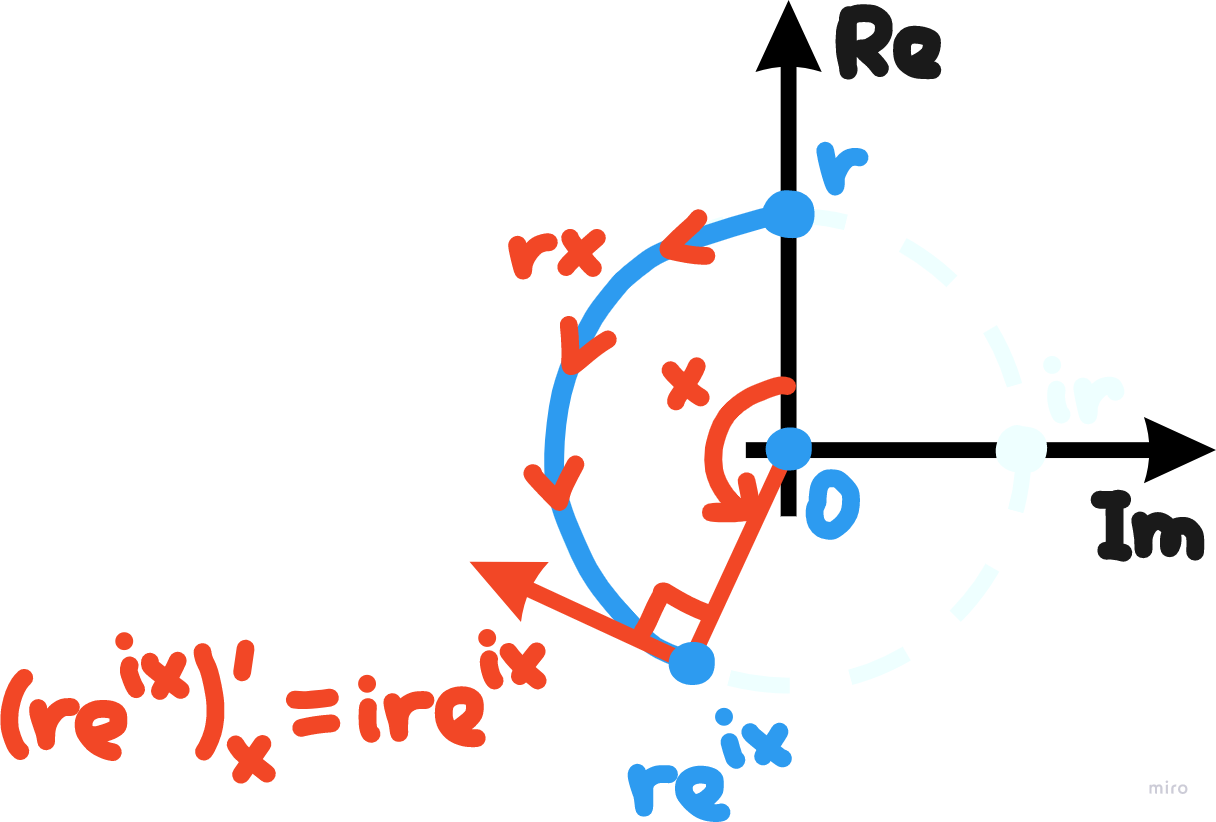
• (e^ix)' = ie^ix.

Первое доказывается тем, что

$x\in \mathbb {R} \Longrightarrow |e^{ix}|^{2}=e^{ix}{\overline {e^{ix}}}=e^{ix}e^{\overline {ix}}=e^{ix-ix}=1.$

Второе же (с учётом, однако, первого) означает, что при положительном движении икса число e^ix будет вращаться по окружности с единичной скоростью в положительном направлении. То есть при вращении от e⁰ⁱ до e^ix экспонента рисует дугу длины |x|. Чтобы снять модуль, введём ориентацию этой дуги: договоримся, что ориентированная длина (x) этой дуги положительна, если при движении икса от 0 до x экспонента двигается сонаправленно своей производной, и отрицательна, если — противонаправленно. Тогда ориентированный угол, на который повращалась эта экспонента, равен x/1 радиан.