Тригонометрия

Титульная страница «Тригонометрии» (переиздание 1612) В. Питиска, давшая название одноименному разделу математики

Суть тригонометрии // Native Code [8:29]

Тригонометрия с нуля за 30 минут // uchus.online [28:46]

Тригонометрия — раздел классической математики, лежащий на пересечении алгебры и геометрии: система законов-функций, по которым на евклидовой плоскости соотносятся стороны и углы треугольников.

Тригонометрия основывается на соотношении подобия. Треугольники с двумя равными углами подобны, поэтому подобны прямоугольные треугольники, в которых равен один острый угол. Отношение длин сторон у подобных треугольников одинаковое, поэтому отношение сторон прямоугольных треугольников зависит только от одного параметра — величины острого угла. Это обстоятельство позволяет обозначить тригонометрические функции: синус, косинус, тангенс, котангенс, секанс и косеканс, через отношение различных сторон прямоугольного треугольника.

Исторические сведения

Некоторые сведения о науке, позже получившей название «тригонометрия», были еще у древних египтян. В папирусе Ахмеса есть пять задач, касающихся измерения пирамид, в которых упоминается какая-то функция угла — «сект». Есть мнение, что «сект» обозначает котангенс угла. Применение этой функции носило сугубо практическую причину: египетские архитекторы строили пирамиды, строго придерживаясь одного и того же значения угла наклона боковой грани к основанию (52°) и угла между ребром и диагональю основания (42°). А для этого надо было знать соответствующие отношения между линейными элементами четырехугольной пирамиды.

Вавилоняне так же имели некоторые знания об этой области математики: они ввели разделение круга на 360° и разделение градуса на 60 частей, что соответствовало принятой в древней Месопотамии шестидесятеричной системе счисления. Для измерения углов вавилоняне пользовались примитивной астролябией.

Древние греки умели решать многие тригонометрические задачи, но они применяли геометрические, а не алгебраические методы.

Тригонометрическую функцию синус впервые ввели древние индийцы в трактате «Сурья-сиддханта». Свойства этой функции исследовал индийский математик 5 века Ариабхата. Дальнейший вклад в развитие тригонометрии сделали арабские математики. До 10 века они апеллировали всеми тригонометрическими функциями и протабулировали их. В Европу понятие тригонометрических функций пришло с переводами трудов ал-Баттани и Ат-Туси. Одной из первых работ европейской математики, посвященных тригонометрии была книга «De Triangulis» немецкого математика 15 века Региомонтана. Однако, еще в 16 веке тригонометрия была мало известна. Коперник вынужден был посвятить ее описанию 2 отдельных раздела в своей работе «Об обращении небесных сфер» (лат. «De revolutionibus orbium coelestium»).

Быстрое дальнейшее развитие тригонометрии было обусловлено требованиями навигации и картографии. Сам термин тригонометрия ввел, опубликовав в 1595 книгу под таким же названием, немецкий математик Варфоломей Питиск (нем. Bartholomäus Pitiscus, 1561—1613). Гемма Фризий описал метод триангуляции.

Со становлением математического анализа тригонометрия получила новые методы. Благодаря трудам Брука Тейлора и Колина Маклорена тригонометрические функции получили представление в виде рядов. Формула Муавра установила связь между тригонометрическими функциями и экспонентой. Леонард Эйлер расширил определение тригонометрических функций на комплексную плоскость.

Тригонометрические функции

Прямоугольный треугольник

• Синус — отношение противолежащего катета к гипотенузе.
• Косинус — отношение прилежащего катета к гипотенузе.
• Тангенс — отношение противолежащего катета к прилежащему.
• Котангенс — отношение прилежащего катета к противолежащему.
• Секанс — отношение гипотенузы к прилежащему катету.
• Косеканс — отношение гипотенузы к противолежащему катету.

Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до $\pi \over 2$ радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол $\theta$ (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:

• Синус угла $\theta$ определяется как ордината точки A.
• Косинус — абсцисса точки A.
• Тангенс — отношение синуса к косинусу.
• Котангенс — отношение косинуса к синусу (то есть величина, обратная тангенсу).
• Секанс — величина, обратная косинусу.
• Косеканс — величина, обратная синусу.

Для острых углов новые определения совпадают с прежними.

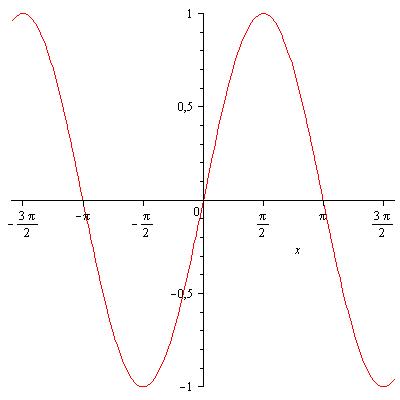
Свойства функции синус

Синус

1. Область определения функции — множество всех действительных чисел: $D(y)=R$.
2. Множество значений — промежуток [−1; 1]: $E(y)$ = [−1;1].
3. Функция $y=\sin \left(\alpha \right)$ является нечётной: $\sin \left(-\alpha \right)=-\sin \alpha$.
4. Функция периодическая, наименьший положительный период равен $2\pi$: $\sin \left(\alpha +2\pi \right)=\sin \left(\alpha \right)$.
5. График функции пересекает ось Ох при $\alpha =\pi n\,,n\in Z$.
6. Промежутки знакопостоянства: $y>0$ при $\left(2\pi n+0;\pi +2\pi n\right)\,,n\in Z$ и $y<0$ при $\left(\pi +2\pi n;2\pi +2\pi n\right)\,,n\in Z$.
7. Функция непрерывна и имеет производную при любом значении аргумента: $(\sin \alpha )'=\cos \alpha$
8. Функция $y=\sin \alpha$ возрастает при $\alpha \in \left(-{\frac {\pi }{2}}+2\pi n;{\frac {\pi }{2}}+2\pi n\right)\,,n\in Z$, и убывает при $\alpha \in \left({\frac {\pi }{2}}+2\pi n;3{\frac {\pi }{2}}+2\pi n\right)\,,n\in Z$.
9. Функция имеет минимум при $\alpha =-{\frac {\pi }{2}}+2\pi n\,,n\in Z$ и максимум при $\alpha ={\frac {\pi }{2}}+2\pi n\,,n\in Z$.

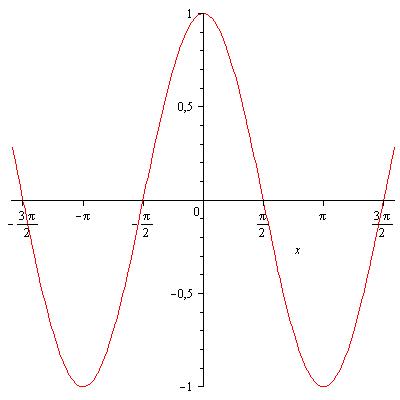
Свойства функции косинус

Косинус

1. Область определения функции — множество всех действительных чисел: $D(y)=R$.
2. Множество значений — промежуток [−1; 1]: $E(y)$ = [−1;1].
3. Функция $y=\cos \left(\alpha \right)$ является чётной: $\cos \left(-\alpha \right)=\cos \alpha$.
4. Функция периодическая, наименьший положительный период равен $2\pi$: $\cos \left(\alpha +2\pi \right)=\cos \left(\alpha \right)$.
5. График функции пересекает ось Ох при $\alpha ={\frac {\pi }{2}}+\pi n\,,n\in Z$.
6. Промежутки знакопостоянства: $y>0$ при $\left(-{\frac {\pi }{2}}+2\pi n;{\frac {\pi }{2}}+2\pi n\right)\,,n\in Z$ и $y<0$ при $\left({\frac {\pi }{2}}+2\pi n;3{\frac {\pi }{2}}+2\pi n\right)\,,n\in Z.$
7. Функция непрерывна и имеет производную при любом значении аргумента: $(\cos \alpha )'=-\sin \alpha$
8. Функция $y=\cos \alpha$ возрастает при $\alpha \in \left(-\pi +2\pi n;2\pi n\right)\,,n\in Z,$ и убывает при $\alpha \in \left(2\pi n;\pi +2\pi n\right)\,,n\in Z.$
9. Функция имеет минимум при $\alpha =\pi +2\pi n\,,n\in Z$ и максимум при $\alpha =2\pi n\,,n\in Z.$

Свойства функции тангенс

Тангенс

1. Область определения функции — множество всех действительных чисел: $D(y)=R$, кроме чисел $\alpha ={\frac {\pi }{2}}+\pi n.$
2. Множество значений — множество всех действительных чисел: $E(y)=R.$
3. Функция $y=\mathrm {tg} \left(\alpha \right)$ является нечётной: $\mathrm {tg} \left(-\alpha \right)=-\mathrm {tg} \ \alpha$.
4. Функция периодическая, наименьший положительный период равен $\pi$: $\mathrm {tg} \left(\alpha +\pi \right)=\mathrm {tg} \left(\alpha \right)$.
5. График функции пересекает ось Ох при $\alpha =\pi n\,,n\in Z$.
6. Промежутки знакопостоянства: $y>0$ при $\left(\pi n;{\frac {\pi }{2}}+\pi n\right)\,,n\in Z$ и $y<0$ при $\left(-{\frac {\pi }{2}}+\pi n;\pi n\right)\,,n\in Z$.
7. Функция непрерывна и имеет производную при любом значении аргумента из области определения: $(\mathop {\operatorname {tg} } \,x)'={\frac {1}{\cos ^{2}x}}.$
8. Функция $y=\mathrm {tg} \ \alpha$ возрастает при $\alpha \in \left(-{\frac {\pi }{2}}+\pi n;{\frac {\pi }{2}}+\pi n\right)\,,n\in Z$.

Свойства функции котангенс

Котангенс

1. Область определения функции — множество всех действительных чисел: $D(y)=R,$ кроме чисел $\alpha =\pi n,n\in \mathbb {Z} \,.$
2. Множество значений — множество всех действительных чисел: $E(y)=R.$
3. Функция $y=\mathop {\operatorname {ctg} } \left(\alpha \right)$ является нечётной: $\mathop {\operatorname {ctg} } \left(-\alpha \right)=-\mathop {\operatorname {ctg} } \ \alpha \,.$
4. Функция периодическая, наименьший положительный период равен $\pi$: $\mathop {\operatorname {ctg} } \left(\alpha +\pi \right)=\mathop {\operatorname {ctg} } \left(\alpha \right).$
5. График функции пересекает ось Ох при $\alpha ={\frac {\pi }{2}}+\pi n\,,n\in \mathbb {Z} \,.$
6. Промежутки знакопостоянства: $y>0$ при $\left(\pi n;{\frac {\pi }{2}}+\pi n\right)\,,n\in \mathbb {Z}$ и $y<0$ при $\left({\frac {\pi }{2}}+\pi n;\pi \left(n+1\right)\right)\,,n\in \mathbb {Z} .$
7. Функция непрерывна и имеет производную при любом значении аргумента из области определения: $(\mathop {\operatorname {ctg} } \,x)'=-{\frac {1}{\sin ^{2}x}}.$
8. Функция $y=\mathop {\operatorname {ctg} } \ \alpha$ убывает при $\alpha \in \left(\pi n;\pi \left(n+1\right)\right)\,,n\in \mathbb {Z} .$

Основные теоремы тригонометрии

Определенные для прямоугольного треугольника тригонометрические функции позволяют решать произвольные треугольники с использованием основных теорем: теоремы синусов, теоремы косинусов и теоремы тангенсов.

Теорема синусов

Теорема синусов утверждает, что отношение синуса угла к длине противоположной стороны треугольника одинакова для всех углов треугольника. Для плоского треугольника со сторонами $a,b,c$ и соответствующими противоположными них углами $A,B,C$ можно записать:

${\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R,$

где $R$ — радиус описанной окружности вокруг треугольника.

$R={\frac {abc}{\sqrt {(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}}.$

Теорема косинусов

По теореме косинусов, квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Для плоского треугольника со сторонами $a,b,c$ и углом $C$, между сторонами $a,b$:

$c^{2}=a^{2}+b^{2}-2ab\cos C,\,$

или:

$\cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}.\,$

Теорема косинусов позволяет определить длину третьей стороны треугольника, если известны длины двух сторон и значение угла между ними.

Теорема тангенсов

Теорема тангенсов — теорема о соотношении между двумя сторонами произвольного треугольника и тангенса полусуммы и полуразности противоположных к ним углов, которая записывается уравнением (формула Региомонтана):

${\frac {a-b}{a+b}}={\frac {\mathop {\operatorname {tg} } \left[{\tfrac {1}{2}}(A-B)\right]}{\mathop {\operatorname {tg} } \left[{\tfrac {1}{2}}(A+B)\right]}}$

Площадь треугольника

Площадь треугольника тоже может быть определена через тригонометрические функции: она равна половине произведения прилегающих сторон на синус угла между ними:

$A={\frac {1}{2}}ab\sin C.\,$

Простейшие тригонометрические уравнения

Уравнения, в которых фигурируют тригонометрические функции, называют тригонометрическими. Самые простые из них имеют аналитические решения, благодаря существованию обратных тригонометрических функций. Поскольку тригонометрические функции периодические, такие решения не единственные, а определяются с точностью до периода.

${\begin{matrix}\sin x=a&(|a|\leq 1)&x=(-1)^{n}\arcsin a+\pi n\\\cos x=a&(|a|\leq 1)&x=\pm \arccos a+2\pi n\\{\text{tg}}\,x=a&&x={\text{arctg}}\,a+\pi n\\{\text{ctg}}\,x=a&&x={\text{arcctg}}\,a+\pi n\\\end{matrix}}$

Формулы преобразования тригонометрических выражений

Синус и косинус суммы/разности:

$\sin(x+y)=\sin x\cos y+\cos x\sin y\!$

$\sin(x-y)=\sin x\cos y-\cos x\sin y\!$

$\cos(x+y)=\cos x\cos y-\sin x\sin y\!$

$\cos(x-y)=\cos x\cos y+\sin x\sin y\!$

Сумма/разность синусов и косинусов:

$\sin x+\sin y=2\sin {\frac {x+y}{2}}\cos {\frac {x-y}{2}}\!$

$\sin x-\sin y=2\sin {\frac {x-y}{2}}\cos {\frac {x+y}{2}}\!$

$\cos x+\cos y=2\cos {\frac {x+y}{2}}\cos {\frac {x-y}{2}}\!$

$\cos x-\cos y=-2\sin {\frac {x+y}{2}}\sin {\frac {x-y}{2}}\!$

Сферическая тригонометрия

Сферическая тригонометрия — раздел сферической геометрии, главными объектами которого являются многоугольники (особенно треугольники) на сфере и соотношение между сторонами и углами. Возникновение сферической геометрии связано с задачами сферической астрономии.

Основными элементами сферической геометрии являются точки и большие круги сферы. Большие круги являются геодезическими линиями сферы, поэтому они в сферической геометрии играют роль, аналогичную роли прямых в планиметрии. Расстояние между двумя точками в сферической геометрии измеряется углом между радиусами сферы, проведенными в эти точки. Угол между двумя «прямыми» равен двугранному углу между плоскостями больших кругов, которые определяют эти «прямые». Две любые «прямые» в сферической геометрии пересекаются в двух точках и разбивают поверхность сферы на 4 двуугольника. Три «прямые», пересекаясь попарно, образуют 8 сферических треугольников. Эти треугольники имеют много необычных свойств, которые отличают их от плоских треугольников. Например, сумма углов сферического треугольника всегда больше 180° и меньше 540°.

Стороны и углы сферического треугольника связаны зависимостями:

${\frac {\sin {\frac {a}{R}}}{\sin A}}={\frac {\sin {\frac {b}{R}}}{\sin B}}={\frac {\sin {\frac {c}{R}}}{\sin C}};$

$\cos {\frac {c}{R}}=\cos {\frac {a}{R}}\cos {\frac {b}{R}}+\sin {\frac {a}{R}}\sin {\frac {b}{R}}\cos C;$

$\cos {\frac {a}{R}}={\frac {\cos A+\cos B\cos C}{\sin B\sin C}}.$

где $a,b,c$ — стороны сферического треугольника; $A,B,C$ — углы, противоположные этим сторонам; $R$ — радиус сферы.

Сферическая тригонометрия очень важна в астрономических вычислениях (небесной механике), а также в орбитальной, космической навигации и навигации на поверхности Земли.

См.также

• Обзор тригонометрии

Литература

• Андронов И. К., Окунев А. К. Курс тригонометрии, развиваемый на основе реальных задач. — М.: Просвещение, 1967. — 648 с.
• Волынский Б. А. Сферическая тригонометрия. — М.: Наука, 1977. — 136 с.
• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1984. — 830 c.

Ссылки

• Динамические математические модели FIZMA.neT
• David Joyce Dave’s Short Course in Trigonometry (Университет Кларка) англ.
• Michael Corral Trigonometry. Covers elementary trigonometry (Distributed under GNU Free Documentation License) англ.