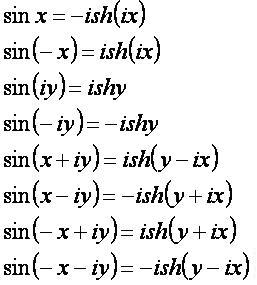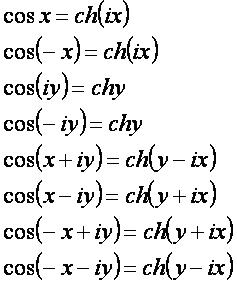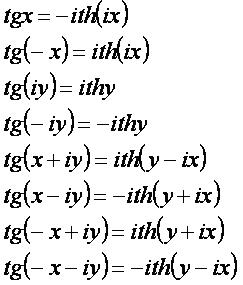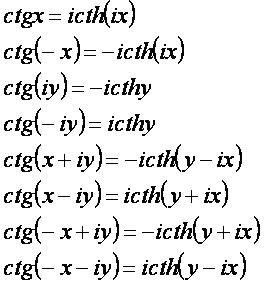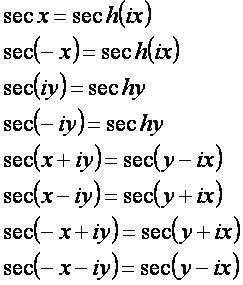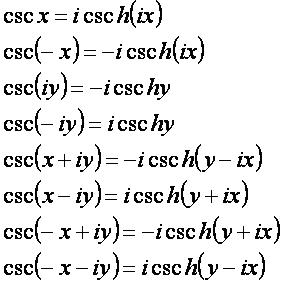Выражение тригонометрических функций через гиперболические
Перейти к навигации
Перейти к поиску
Выражение тригонометрических функций через гиперболические функции — это формулы, выражающие каждую из основных тригонометрических функций через гиперболические функции.
Обозначения[править]
Введём обозначения:
x — действительная часть (абсцисса) переменной;
y — мнимая часть (ордината) переменной;
α = x + iy — комплексная переменная.
Формулы[править]
sinα[править]
cosα[править]
tgα[править]
ctgα[править]
secα[править]
cscα[править]
См. также[править]
- Выражение гиперболических функций через тригонометрические
- Логарифм комплексного числа
- Формулы эквивалентных преобразований для тригонометрических функций
Другие формулы[править]
- тригонометрические функции;
- сумма тригонометрических функций;
- разность тригонометрических функций;
- произведение тригонометрических функций;
- тригонометрические функции суммы углов;
- тригонометрические функции разности углов;
- тригонометрические формулы приведения;
- тригонометрические функции кратных углов;
- тригонометрические функции половинного угла;
- тригонометрические функции угла, полученного многократным делением пи на два;
- выражение тригонометрических функций через другую;
- выражение тригонометрических функций через гиперболические;
- тригонометрические функции комплексной переменной;
- производные тригонометрических функций;
- дифференциалы тригонометрических функций;
- интегралы тригонометрических функций;
- графики тригонометрических функций.
Литература[править]
- Бронштейн М. Н., Семендяев К. А. Справочник по математике. М., 1956, стр.195.
